题目内容
因式分解：
（1）（a2+2a）2-7（a2+2a）-8
（2）x3-3x2+3x-1
（3）k3-3k+2．
（1）（a2+2a）2-7（a2+2a）-8
（2）x3-3x2+3x-1
（3）k3-3k+2．
考点：二次函数的性质
专题：计算题
分析：（1）将a2+2a看成一个整体，可将（a2+2a）2-7（a2+2a）-8分解为（a2+2a-8）（a2+2a+1）的形式，进而根据十字相乘法和公式法，可继续分解；
（2）利用分组分解法，将x3-3x2+3x-1分成两组（x3-1）-（3x2-3x）的形式，分别采用立方差公式和提取公因式法，可将原不等式进行分解；
（3）利用补项法，将k3-3k+2化为k3-k2+k2-3k+2，并将前两项和后三项分为两组，分别采用提取公因式法和十字分解法，可将原不等式进行分解；
（2）利用分组分解法，将x3-3x2+3x-1分成两组（x3-1）-（3x2-3x）的形式，分别采用立方差公式和提取公因式法，可将原不等式进行分解；
（3）利用补项法，将k3-3k+2化为k3-k2+k2-3k+2，并将前两项和后三项分为两组，分别采用提取公因式法和十字分解法，可将原不等式进行分解；
解答：
解：（1）（a2+2a）2-7（a2+2a）-8
=（a2+2a-8）（a2+2a+1）
=（a+4）（a-2）（a+1）2；-----------（4分）
（2）x3-3x2+3x-1
=（x3-1）-（3x2-3x）
=（x-1）（x2+x+1）-3x（x-1）
=（x-1）（x2-2x+1）
=（x-1）3-----------（5分）
（3）k3-3k+2
=k3-k2+k2-3k+2
=k2（k-1）+（k-1）（k-2）
=（k-1）（k2+k-2）
=（k-1）（k-1）（k+2）
=（k-1）2（k+2）-----------（5分）
=（a2+2a-8）（a2+2a+1）
=（a+4）（a-2）（a+1）2；-----------（4分）
（2）x3-3x2+3x-1
=（x3-1）-（3x2-3x）
=（x-1）（x2+x+1）-3x（x-1）
=（x-1）（x2-2x+1）
=（x-1）3-----------（5分）
（3）k3-3k+2
=k3-k2+k2-3k+2
=k2（k-1）+（k-1）（k-2）
=（k-1）（k2+k-2）
=（k-1）（k-1）（k+2）
=（k-1）2（k+2）-----------（5分）
点评：本题考查的知识点是因式分解法，熟练掌握因式分解法中十字相乘法，分组分解法，补项法等方法是解答的关键．
练习册系列答案
相关题目
函数f（x）由下表定义：
若a1=2，an+1=f（an），n=l，2，3，…，则数列{an}的前2010项的和S2010=（ ）
| x | 1 | 2 | 3 | 4 | 5 |
| F（x） | 4 | 1 | 3 | 5 | 2 |
| A、6021 | B、6023 |
| C、6025 | D、6027 |
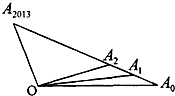如图，O为线段A0A2013外一点，若A0，A1，A2，A3，…，A2013中任意相邻两点的距离相等，| OA0 |
| a |
| OA2013 |
| b |
| a |
| b |
| OA0 |
| OA1 |
| OA2 |
| OA2013 |
A、1006（
| ||||
B、1007（
| ||||
C、2012（
| ||||
D、2014（
|
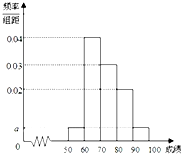某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．
已知