题目内容
4.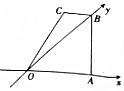 用斜二测画法得到一个水平放置的平面图形的直观图为如图所示的直角梯形,其中梯形的上底是下底的$\frac{1}{2}$,若原平面图形的面积为3$\sqrt{2}$,则OA的长为( )
用斜二测画法得到一个水平放置的平面图形的直观图为如图所示的直角梯形,其中梯形的上底是下底的$\frac{1}{2}$,若原平面图形的面积为3$\sqrt{2}$,则OA的长为( )| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{3\sqrt{2}}{2}$ |
分析 由题意,原平面图形与斜二测画法得到的直观图的面积比为$1:\frac{\sqrt{2}}{4}$,利用原平面图形的面积为3$\sqrt{2}$,求出OA的长.
解答 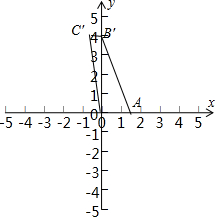 解:由题意,原平面图形与斜二测画法得到的直观图的面积比为$1:\frac{\sqrt{2}}{4}$,
解:由题意,原平面图形与斜二测画法得到的直观图的面积比为$1:\frac{\sqrt{2}}{4}$,
设OA=x,则直观图的面积为$\frac{1}{2}x•(x+\frac{x}{2})=\frac{3}{4}{x}^{2}$,
∴2$\sqrt{2}×\frac{3}{4}{x}^{2}$=3$\sqrt{2}$,∴$x=\sqrt{2}$.
故选B.
点评 由已知斜二测直观图根据斜二测画法规则正确画出原平面图形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.若圆C:x2+y2-2(m-1)x+2(m-1)y+2m2-6m+4=0过坐标原点,则实数m的值为( )
| A. | 2或1 | B. | -2或-1 | C. | 2 | D. | 1 |
15.已知全集U=R,集合A={x|x<2},集合B={x|x>1},则(∁UA)∩B=( )
| A. | {x|1<x<2} | B. | {x|x≥2} | C. | {x|1≤x<2} | D. | {x|x≤1} |
12.数列{an}满足${a_1}+3{a_2}+{3^2}{a_3}+…+{3^{n-1}}{a_n}=\frac{n}{2}$,则an=( )
| A. | $\frac{1}{{3•{2^{n-1}}}}$ | B. | $\frac{1}{{2•{3^{n-1}}}}$ | C. | $\frac{1}{2^n}$ | D. | $\frac{n}{3^n}$ |
16.设集合A={x|2x≥4},集合B={x|y=lg(x-1)},则A∩B=( )
| A. | [1,2) | B. | (1,2] | C. | [2,+∞) | D. | [1,+∞) |