类比等差数列.定义“等和数列 :在一个数列中.如果每一项与它的后一项的和都为同一个常数.那么这个数列叫做等和数列.这个常数叫做该数列的公和．已知数列{an}是等和数列.且a1=2.公和为5.则这个数列的前2017项和S2017=5042．题目和参考答案——青夏教育精英家教网—

题目内容

15．类比等差数列，定义“等和数列”：在一个数列中，如果每一项与它的后一项的和都为同一个常数，那么这个数列叫做等和数列，这个常数叫做该数列的公和．已知数列{a_n}是等和数列，且a₁=2，公和为5，则这个数列的前2017项和S₂₀₁₇=5042．

分析根据“等和数列”的定义可知a_n+a_n+1=5，n∈N*，从而可得前2017项的和，然后利用分组求和法进行求解即可．

解答解：由题意知，a_n+a_n+1=5，n∈N*，且a₁=2，
所以，a₁+a₂=5，得a₂=3，a₃=2，a₄=3，…a₂₀=3，a₂₁=2，…，
∴S₂₀₁₇=（2+3）+（2+3）+…（2+3）+2=5×1008+2=5042．
故答案为：5042．

点评本题主要由新定义考查数列的求和，该题采用分组求和进行求解，同时考查运算求解的能力，属于基础题．

练习册系列答案

相关题目

4．

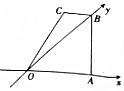用斜二测画法得到一个水平放置的平面图形的直观图为如图所示的直角梯形，其中梯形的上底是下底的$\frac{1}{2}$，若原平面图形的面积为3$\sqrt{2}$，则OA的长为（　　）

$\frac{3\sqrt{2}}{2}$

6．已知点F₂，P分别为双曲线$\frac{{x}^{2}}{{a\;}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点与右支上的一点，O为坐标原点，若$\overrightarrow{OM}$=$\frac{1}{2}$（$\overrightarrow{OP}$+$\overrightarrow{O{F}_{2}}$），${\overrightarrow{O{F}_{2}}}^{2}$=${\overrightarrow{{F}_{2}M}}^{2}$且2$\overrightarrow{O{F}_{2}}$•$\overrightarrow{{F}_{2}M}$=a²+b²，则该双曲线的离心率为（　　）

A．

$\frac{\sqrt{3}+1}{2}$

3．已知f（tanx）=sin²x-sinx•cosx，则f（2）=（　　）

10．已知函数f（x）=alnx+$\frac{a+1}{2}{x^2}$+1．
（1）当a=-$\frac{1}{2}$时，求f（x）在区间$[{\frac{1}{e}，e}]$上的最大值与最小值；
（2）讨论函数f（x）的单调性；
（3）当-1＜a＜0时，任意x＞0有f（x）＞1+$\frac{a}{2}ln（{-a}）$恒成立，求a的取值范围．

20．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0），过C上一点$（{2\sqrt{2}，\sqrt{2}}）$的切线l的方程为x+2y-4$\sqrt{2}$=0．
（1）求椭圆C的方程．
（2）设过点M（0，1）且斜率不为0的直线交椭圆于A，B两点，试问y轴上是否存在点P，使得$\overrightarrow{PM}=λ（\frac{{\overrightarrow{PA}}}{{|{\overrightarrow{PA}}|}}+\frac{{\overrightarrow{PB}}}{{|{\overrightarrow{PB}}|}}）$？若存在，求出点P的坐标；若不存在说明理由．

7．已知sin θ、cos θ是关于x的方程x²-ax+a=0的两个根（a∈R）．
（1）求sin³θ+cos³θ的值；
（2）求tan θ+$\frac{1}{tanθ}$的值．

4．已知函数f（x）=cos²x+asinx+2a-1，a∈R．
（1）当a=1时，求函数的最值并求出对应的x值；
（2）如果对于区间$[-\frac{π}{2}，\frac{π}{2}]$上的任意一个x，都有f（x）≤5恒成立，求a的取值范围．

5．已知函数f（x）=$\frac{2lnx+{a}^{2}}{x}$+bx-2a（a∈R），其中b=${∫}_{0}^{\frac{π}{2}}$（2sin$\frac{t}{2}$•cos$\frac{t}{2}$）dt，若?x∈（1，2），使得f′（x）•x+f（x）＞0成立，则实数a的取值范围为（　　）

试题分类