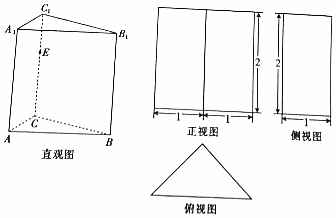
题目内容
16．设集合A={x|2x≥4}，集合B={x|y=lg（x-1）}，则A∩B=（ ）| A． | [1，2） | B． | （1，2] | C． | [2，+∞） | D． | [1，+∞） |
分析 先分别求出集合A和集合B，由此利用交集定义能求出A∩B．
解答 解：∵集合A={x|2x≥4}={x|x≥2}，
集合B={x|y=lg（x-1）}={x＞1}，
∴A∩B={x|x≥2}=[2，+∞）．
故选：C．
点评 本题考查交集的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．
练习册系列答案
相关题目
4．
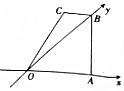用斜二测画法得到一个水平放置的平面图形的直观图为如图所示的直角梯形，其中梯形的上底是下底的$\frac{1}{2}$，若原平面图形的面积为3$\sqrt{2}$，则OA的长为（ ）
用斜二测画法得到一个水平放置的平面图形的直观图为如图所示的直角梯形，其中梯形的上底是下底的$\frac{1}{2}$，若原平面图形的面积为3$\sqrt{2}$，则OA的长为（ ）| A． | 2 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | $\frac{3\sqrt{2}}{2}$ |
1．设复数z=-7+5i（是虚数单位），z的共轭复数为$\overline{z}$，则复数（6+z）•$\overline{z}$的虚部为（ ）
| A． | -30 | B． | 30 | C． | 32 | D． | -32 |
6．已知点F2，P分别为双曲线$\frac{{x}^{2}}{{a\;}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点与右支上的一点，O为坐标原点，若$\overrightarrow{OM}$=$\frac{1}{2}$（$\overrightarrow{OP}$+$\overrightarrow{O{F}_{2}}$），${\overrightarrow{O{F}_{2}}}^{2}$=${\overrightarrow{{F}_{2}M}}^{2}$且2$\overrightarrow{O{F}_{2}}$•$\overrightarrow{{F}_{2}M}$=a2+b2，则该双曲线的离心率为（ ）
| A． | $\frac{\sqrt{3}+1}{2}$ | B． | $\frac{3}{2}$ | C． | $\sqrt{3}$ | D． | 2$\sqrt{3}$ |