题目内容
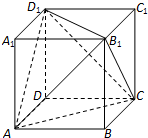 如图,已知正方体ABCD-A1B1C1D1的棱长为1.
如图,已知正方体ABCD-A1B1C1D1的棱长为1.(Ⅰ)求四面体D1-AB1C的左视图的面积;
(Ⅱ)求四面体D1-AB1C的体积.
考点:简单空间图形的三视图,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)分别作点A,D1在平面BCC1B1内的投影,即得左视图,从而得其面积;
(2)将四面体D1-AB1C看作是一个三棱锥,把正方体的体积分割成五部分,所求体积为正方体体积与四个三棱锥的体积之差.
(2)将四面体D1-AB1C看作是一个三棱锥,把正方体的体积分割成五部分,所求体积为正方体体积与四个三棱锥的体积之差.
解答:
解:(Ⅰ)点D1在平面BCC1B1内的投影为点C1,点A在平面BCC1B1内的投影为点B,
所以四面体D1-AB1C的左视图是一个与正方形BCC1B1全等的正方形,其面积为1.
(Ⅱ)∵VB-B1AC=VA1-AB1D1=VD-D1AC=VC1-B1D1C=
×
×1×1×1=
,
∴四面体D1-AB1C的体积为VD1-AB1C=VABCD-A1B1C1D1-4VB-B1AC=13-4×
=
.
所以四面体D1-AB1C的左视图是一个与正方形BCC1B1全等的正方形,其面积为1.
(Ⅱ)∵VB-B1AC=VA1-AB1D1=VD-D1AC=VC1-B1D1C=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
∴四面体D1-AB1C的体积为VD1-AB1C=VABCD-A1B1C1D1-4VB-B1AC=13-4×
| 1 |
| 6 |
| 1 |
| 3 |
点评:本题考查学生的空间想象力与化归思想的运用,三棱锥(或四面体)的体积计算公式,体积分割法处理体积问题等,题目较容易.平时应掌握一些常见的几何模型,如三棱锥(或四面体)、正方体的特征,体积与面积的计算方法等.

练习册系列答案
相关题目
函数y=4x4+4x2+1的导数是( )
| A、16x3+4x2 |
| B、4x3+8x |
| C、16x3+8x |
| D、16x3+4x |
设直线y=
x与圆C:(x-2)2+y2=4交于A,B两点,则弦长|AB|=( )
| 3 |
A、
| ||
B、2
| ||
| C、1 | ||
| D、2 |