题目内容
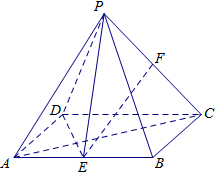如图，四棱锥P-ABCD的底面为矩形，AB=| 2 |
（Ⅰ）求证：EF∥平面PAD；
（Ⅱ）求证：平面PAC⊥平面PDE．
考点：平面与平面垂直的判定,直线与平面平行的判定
专题：证明题,空间位置关系与距离
分析：（Ⅰ）取PD中点G，连AG，FG，证明四边形AEFG为平行四边形，可得EF∥AG，即可证明EF∥平面PAD；
（Ⅱ）证明DE⊥平面PAC，再证明平面PAC⊥平面PDE．
（Ⅱ）证明DE⊥平面PAC，再证明平面PAC⊥平面PDE．
解答：
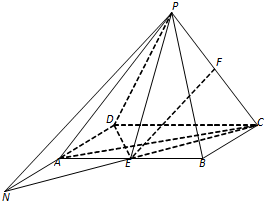证明：（Ⅰ）取PD中点G，连AG，FG，
因为F、G分别为PC、PD的中点，
所以FG∥CD，且FG=
CD．…（2分）
又因为E为AB中点，所以AE∥CD，且AE=
CD．…（3分）
所以AE∥FG，AE=FG．
故四边形AEFG为平行四边形． …（5分）
所以EF∥AG，
又EF?平面PAD，AG?平面PAD，
故EF∥平面PAD． …（7分）
（Ⅱ）设AC∩DE=G，由△AEG∽△CDG及E为AB中点得
=
=
，
又因为AB=
，BC=1，所以AC=
，AG=
AC=
．
所以
=
=
，
又∠BAC为公共角，所以△GAE∽△BAC．
所以∠AGE=∠ABC=90°，即DE⊥AC． …（10分）
又DE⊥PA，PA∩AC=A，
所以DE⊥平面PAC． …（12分）
又DE?平面PDE，所以平面PAC⊥面PDE． …（14分）
证明：（Ⅰ）取PD中点G，连AG，FG，因为F、G分别为PC、PD的中点，
所以FG∥CD，且FG=
| 1 |
| 2 |
又因为E为AB中点，所以AE∥CD，且AE=
| 1 |
| 2 |
所以AE∥FG，AE=FG．
故四边形AEFG为平行四边形． …（5分）
所以EF∥AG，
又EF?平面PAD，AG?平面PAD，
故EF∥平面PAD． …（7分）
（Ⅱ）设AC∩DE=G，由△AEG∽△CDG及E为AB中点得
| AG |
| CG |
| AE |
| CD |
| 1 |
| 2 |
又因为AB=
| 2 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
所以
| AG |
| AE |
| AB |
| AC |
| ||
|
又∠BAC为公共角，所以△GAE∽△BAC．
所以∠AGE=∠ABC=90°，即DE⊥AC． …（10分）
又DE⊥PA，PA∩AC=A，
所以DE⊥平面PAC． …（12分）
又DE?平面PDE，所以平面PAC⊥面PDE． …（14分）
点评：本题以四棱锥为例，考查了空间的直线与平面平行的判定，以及平面与平面垂直的判定，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目