题目内容
设函数f(x)=x2+
(x≠0),当a>1时,方程f(x)=f(a)的实根个数为 .
| 2 |
| x |
考点:根的存在性及根的个数判断
专题:计算题,作图题,函数的性质及应用
分析:求导确定函数的单调性,并作出其简图,由图可得答案.
解答:
解:f′(x)=2x-
,
①当x>1,即f′(x)>0时,函数f(x)=x2+
在(1,+∞)上是增函数,
②当0<x<1时,f′(x)<0,函数f(x)=x2+
在(0,1)上是减函数,
③当x<0时,f′(x)<0,函数f(x)=x2+
在(-∞,0)上是减函数,
作出其简图如下图:
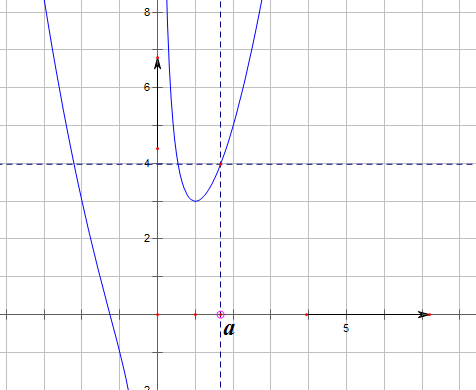
则方程方程f(x)=f(a)的实根个数为3个.
故答案为:3.
| 2 |
| x2 |
①当x>1,即f′(x)>0时,函数f(x)=x2+
| 2 |
| x |
②当0<x<1时,f′(x)<0,函数f(x)=x2+
| 2 |
| x |
③当x<0时,f′(x)<0,函数f(x)=x2+
| 2 |
| x |
作出其简图如下图:

则方程方程f(x)=f(a)的实根个数为3个.
故答案为:3.
点评:本题考查了方程的根与函数的零点的关系,同时考查了数形结合的思想及学生作图的能力,属于中档题.

练习册系列答案
相关题目
若函数y=x-2的值域为[-3,2],则它的定义域为( )
| A、{x|x≤0} |
| B、{x|x≤-1} |
| C、(-1,0) |
| D、[-1,4] |
已知命题p:若(x-1)(x-2)≠0,则x≠1或x≠2;命题q:存在实数x0,使2x0<0.下列选项中为真命题的是( )
| A、p | B、¬q | C、p∨q | D、q∧p |
过原点的直线l与曲线C:
+y2=1相交,若直线l被曲线C所截得的线段长不大于
,则直线l的倾斜角α的取值范围是( )
| x2 |
| 3 |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
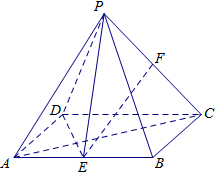 如图,四棱锥P-ABCD的底面为矩形,AB=
如图,四棱锥P-ABCD的底面为矩形,AB=