题目内容
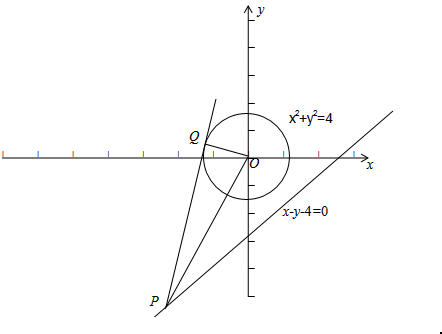
已知圆C:x2+y2=4,点P(x0,y0)在直线x-y-4=0上,O为坐标原点,若圆C上存在点Q,使∠OPQ=30°,则x0的取值范围是 .
考点:直线和圆的方程的应用
专题:直线与圆
分析:因为O是圆心,Q是圆上的点,则∠OPQ以PQ为切线时最大,在直角三角形POQ中,直角边OQ=2是定值,因此当PQ为切线时,且∠OPQ=30°时P点的位置(左右两个点)为边界位置,其它符合题意的点都介于这两个点之间,据此求解.
解答:
解:由O是圆心,Q是圆上的点,则∠OPQ以PQ为切线时最大,在直角三角形POQ中,直角边OQ=2是定值,因此当PQ为切线时,且∠OPQ=30°时P点的位置(左右两个点)为边界位置,其它符合题意的点都介于这两个点之间.
此时,在三角形POQ中,因为∠OPQ=30°,且OQ=2,所以sin∠OPQ=
=
,
故OP=4,设P(x0,x0-4),所以OP=
,
解得x0=0或x0=4.
故x0的范围是[0,4].
故答案为:[0,4].
此时,在三角形POQ中,因为∠OPQ=30°,且OQ=2,所以sin∠OPQ=
| OQ |
| OP |
| 1 |
| 2 |
故OP=4,设P(x0,x0-4),所以OP=
| x02+(x0-4)2 |
解得x0=0或x0=4.
故x0的范围是[0,4].
故答案为:[0,4].

点评:本题考查了圆的几何性质,通过分析先将问题转化为圆的切线问题,最终化成点到直线的距离问题.

练习册系列答案
相关题目
已知命题p:若(x-1)(x-2)≠0,则x≠1或x≠2;命题q:存在实数x0,使2x0<0.下列选项中为真命题的是( )
| A、p | B、¬q | C、p∨q | D、q∧p |
已知0<k<
,则关于x的方程
=kx的实数解的个数是( )
| 1 |
| 3 |
| |2-x| |
| A、1个 | B、2个 | C、3个 | D、4个 |
已知双曲线C:
-
=1(a>0,b>0)的右焦点为F,若过点F且倾斜角为45°的直线与双曲线的右支有且只有一个交点,则此双曲线的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、[
| ||
B、(
| ||
| C、(2,+∞) | ||
| D、(1,+∞) |
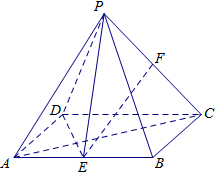 如图,四棱锥P-ABCD的底面为矩形,AB=
如图,四棱锥P-ABCD的底面为矩形,AB=