题目内容
已知△ABC中，BC=3，AC=4，AB=5，点P是三条边上的任意一点，m=
•
，则m的最小值是 ．
| PA |
| PB |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由已知条件得△ABC为直角三角形，当P点和A，B，C三点重合时，容易求出m=0．当P点在BC边上，且不与B，C重合时，设
=x
，
=
+
=x
+
-
=(x-1)
+
，所以m=
•
=x
•[(x-1)
+
]=9x(x-1)=9[(x-
)2-
]≥-
，即此时m的最小值是-
，用同样的方法求P点在另外两边时m的最小值，找出最小的m即可．
| PB |
| CB |
| PA |
| PB |
| BA |
| CB |
| CA |
| CB |
| CB |
| CA |
| PA |
| PB |
| CB |
| CB |
| CA |
| 1 |
| 2 |
| 1 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
解答：
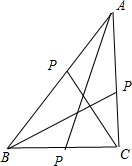解：由三条边的长度知，△ABC为直角三角形，如图所示，容易求得当P点在A，B，C三点时，m=
•
=0；
当点P在B，C点之间时，设
=x
，
=
+
=x
+
-
=(x-1)
+
；
∴m=
•
=x
•[(x-1)
+
]=x(x-1)
2=9[(x-
)2-
]≥-
；
当点P在点A，C之间时，设
=x
，
=
+
=x
+
-
=(x-1)
+
；
∴m=
•
=x
•[(x-1)
+
]=x(x-1)
2=16[(x-
)2-
]≥-4；
当点P在点A，B之间时，设
=x
，则
=-(1-x)
；
∴m=
•
=x(x-1)
2=25[(x-
)2-
]≥-
；
综上得m的最小值为-
．
故答案为：-
．
解：由三条边的长度知，△ABC为直角三角形，如图所示，容易求得当P点在A，B，C三点时，m=| PA |
| PB |
当点P在B，C点之间时，设
| PB |
| CB |
| PA |
| PB |
| BA |
| CB |
| CA |
| CB |
| CB |
| CA |
∴m=
| PA |
| PB |
| CB |
| CB |
| CA |
| CB |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
当点P在点A，C之间时，设
| PA |
| CA |
| PB |
| PA |
| AB |
| CA |
| CB |
| CA |
| CA |
| CB |
∴m=
| PA |
| PB |
| CA |
| CA |
| CB |
| CA |
| 1 |
| 2 |
| 1 |
| 4 |
当点P在点A，B之间时，设
| PA |
| BA |
| PB |
| BA |
∴m=
| PA |
| PB |
| BA |
| 1 |
| 2 |
| 1 |
| 4 |
| 25 |
| 4 |
综上得m的最小值为-
| 25 |
| 4 |
故答案为：-
| 25 |
| 4 |
点评：考查两向量垂直时，数量积为0，共线向量基本定理，向量的加法，向量的减法，配方法求二次函数的最小值．
练习册系列答案
名校课堂系列答案
相关题目
若函数y=x-2的值域为[-3，2]，则它的定义域为（ ）
| A、{x|x≤0} |
| B、{x|x≤-1} |
| C、（-1，0） |
| D、[-1，4] |
在直二面角α-l-β的棱l上取一点A、过A分别在α，β内A的同侧作与l成45°的直线，则这两条直线所夹的角为（ ）
| A、45° | B、60° |
| C、90° | D、120° |
已知命题p：若（x-1）（x-2）≠0，则x≠1或x≠2；命题q：存在实数x0，使2x0＜0．下列选项中为真命题的是（ ）
| A、p | B、￢q | C、p∨q | D、q∧p |
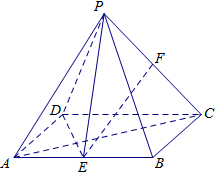如图，四棱锥P-ABCD的底面为矩形，AB=