题目内容
直三棱柱ABC-A′B′C′各侧棱和底面边长均为a,点D是CC′上任意一点,连结A′B,BD,A′D,AD,则三棱锥A-A′BD的体积( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:由已知得△AA′D的面积=△AA′C的面积=
AC×AA′=
,B到平面AA′D的距离=B到AC的距离=
AB=
a,由此能求出三棱锥A-A′BD的体积.
| 1 |
| 2 |
| a2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
解答:
解:∵ABC-A′B′C′是直三棱柱,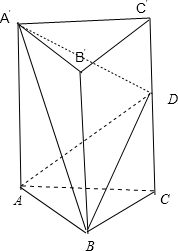
∴AC⊥AA′,AA′∥CD,
∴△AA′D的面积=△AA′C的面积=
AC×AA′=
,
∵ABC-A′B′C′是直三棱柱,
∴B到平面AA′D的距离=B到AC的距离=
AB=
a,
∴三棱锥A-A′BD的体积:
V=
×
×
=
a3.
故选:C.

∴AC⊥AA′,AA′∥CD,
∴△AA′D的面积=△AA′C的面积=
| 1 |
| 2 |
| a2 |
| 2 |
∵ABC-A′B′C′是直三棱柱,
∴B到平面AA′D的距离=B到AC的距离=
| ||
| 2 |
| ||
| 2 |
∴三棱锥A-A′BD的体积:
V=
| 1 |
| 3 |
| a2 |
| 2 |
| ||
| 2 |
| ||
| 12 |
故选:C.
点评:本题考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
计算:i(i+1)=( )
| A、i+1 | B、i-1 |
| C、-i+1 | D、-i-1 |
四面体S-ABC中,已知SA⊥AB,AB⊥BC,|
|=3,|
|=4,|
|=5,|
|=
,则二面角S-AB-C的大小为( )
| SA |
| AB |
| BC |
| SC |
| 35 |
A、
| ||
B、
| ||
C、
| ||
D、
|
由6个座位连成一排,现有3人就坐,则恰有两个空座位相邻的不同坐法有( )
| A、36种 | B、48种 |
| C、72种 | D、96种 |
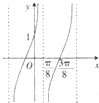 已知函数f(x)=Atan(ωx+φ)(ω>0,|φ|<
已知函数f(x)=Atan(ωx+φ)(ω>0,|φ|<| π |
| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、kπ+
| ||||
D、
|