题目内容
19．等差数列{an}中，a3=7，a5=a2+6，则{an}的通项公式为an=2n+1．分析 利用等差数列的通项公式即可得出．
解答 解：设等差数列{an}公差为d，∵a3=7，a5=a2+6，
∴$\left\{\begin{array}{l}{{a}_{1}+2d=7}\\{{a}_{1}+4d={a}_{1}+d+6}\end{array}\right.$，
解得d=2，a1=3．
∴an=3+2（n-1）=2n+1．
故答案为：an=2n+1．
点评 本题考查了等差数列的通项公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
10．设$a={（\frac{1}{2}）^{2.5}}，b={（2.5）^0}，c={2^{2.5}}$，则（ ）
| A． | a＞b＞c | B． | b＞a＞c | C． | c＞b＞a | D． | b＞c＞a |
7．
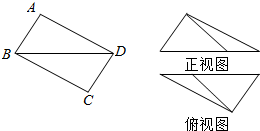如图，在矩形ABCD中，$AB=\frac{3}{2}，BC=2$，沿BD将矩形ABCD折叠，连接AC，所得三棱锥A-BCD的正视图和俯视图如图所示，则三棱锥A-BCD的侧视图的面积为（ ）
如图，在矩形ABCD中，$AB=\frac{3}{2}，BC=2$，沿BD将矩形ABCD折叠，连接AC，所得三棱锥A-BCD的正视图和俯视图如图所示，则三棱锥A-BCD的侧视图的面积为（ ）| A． | $\frac{9}{25}$ | B． | $\frac{12}{5}$ | C． | $\frac{18}{25}$ | D． | $\frac{36}{25}$ |
如图，靠山有一个水库，某人先从水坝的底部A测得水坝对面的山顶P的仰角为40°，再沿坝面向上走80米到水坝的顶部B测得∠ABP=56°，若坝面与水平面所成的锐角为30°，则山高为176米；（结果四舍五入取整）
9．函数f（x）=x2+x-lnx的零点的个数是（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |