题目内容

8．求（x-$\frac{1}{x}$）10的二项展开式中含有x2的项．

分析 先求出二项式展开式的通项公式，再令x的幂指数等于2，求得r的值，即可求得展开式中含有x2的项．

解答 解：由于（x-$\frac{1}{x}$）10的二项展开式的通项公式为 Tr+1=${C}_{10}^{r}$•（-1）r•x10-2r，
令10-2r=2，求得 r=4，
∴展开式中x2的系数是${C}_{10}^{4}$=210，
故（x-$\frac{1}{x}$）10的二项展开式中含有x2的项为210x2．

点评 本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公式，求展开式中某项的系数，属于基础题．

练习册系列答案
相关题目
18．在△ABC中，角A，B，C所对的边分别为a，b，c，向量$\overrightarrow{m}$=（2，cos2C-1），$\overrightarrow{n}$=（sin2$\frac{A+B}{2}$，1）且$\overrightarrow{m}$⊥$\overrightarrow{n}$．
（1）求角C的大小；
（2）如果△ABC的外接圆的半径为1，求△ABC的面积的最大值．
19．等差数列{an}中，a3=7，a5=a2+6，则{an}的通项公式为an=2n+1．
16．己知函数f（x）=x-a1nx（a≠0，a∈R）．
（Ⅰ）讨论f（x）的极值；
（Ⅱ）设A（x1，f（x1）），B（x2，f（x2））（0＜x1＜x2）是曲线y=f（x）上不同两点，若存在t∈（x1，x2），使得y=f（x）在（t，f（t））处的切线与直线AB平行，求证：t＜$\frac{{x}_{1}+{x}_{2}}{2}$．
3．若数列{an}满足a1=1，a2=2，an=an-1+an-2（n∈N*，n＞2），则a6=（　　）
A．13B．8C．21D．10
13．某几何体的三视图如图所示，方格纸中小正方形的边长为1，则此几何体的体积为（　　）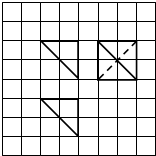
A．$\frac{4}{3}$B．$\frac{2}{3}$C．2D．4
20．抛物线C：y2=4x上一点P到焦点F的距离为5，则点P的坐标为（　　）
A．（1，2）B．（2，2$\sqrt{2}$）C．（3，2$\sqrt{3}$）D．（4，±4）
17．函数f（x）=$\sqrt{sinx-\frac{1}{2}}$，x∈（0，2π）的定义域是[$\frac{π}{6}$，$\frac{5π}{6}$]．
18．已知x、y∈（-2，2）且xy=1，则$\frac{2}{2-{x}^{2}}$+$\frac{4}{4-{y}^{2}}$的最小值为$\frac{16+4\sqrt{2}}{7}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网