题目内容
已知函数f(x)满足:①对任意x∈(0,+∞),恒有f(2x)=2f(x);②当x∈(1,2]时,f(x)=2-x.则f(8)= ;方程f(x)=
的最小正数解为 .
| 1 |
| 5 |
考点:抽象函数及其应用
专题:计算题,函数的性质及应用
分析:根据条件求出f(2)=0,令x=2,求出f(4),令x=4,求出f(8);令
<x≤1,转化到已知范围,从而求出f(x)的解析式,同理分别求出
<x≤
,
<x≤
,
<x≤
时的解析式,令f(x)=
,分别求出x,并检验即得结果.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 4 |
| 1 |
| 16 |
| 1 |
| 8 |
| 1 |
| 5 |
解答:
解:∵当x∈(1,2]时,f(x)=2-x,
∴f(2)=0,
∵?x>0,f(2x)=2f(x),
∴f(4)=2f(2)=0,f(8)=2f(4)=0;
令
<x≤1,则1<2x≤2,
∴f(2x)=2-2x,
又f(2x)=2f(x),
∴当
<x≤1时,f(x)=1-x,
令
<x≤
,则
<2x≤1,f(2x)=1-2x,
又f(2x)=2f(x),
∴当
<x≤
时,f(x)=
-x,
令
<x≤
,则
<2x≤
,f(2x)=
-2x,
又f(2x)=2f(x),
∴当
<x≤
时,f(x)=
-x,
同理可得:当
<x≤
时,f(x)=
-x,
令f(x)=
,则由2-x=
,得x1=
,
由1-x=
,得x2=
,
由
-x=
,得x3=
,
由
-x=
,得x4=
∉(
,
],
由
-x=
,得x5<0,
可推出以下都小于0.
∴方程f(x)=
的最小正数解为
.
故答案为:0,
.
∴f(2)=0,
∵?x>0,f(2x)=2f(x),
∴f(4)=2f(2)=0,f(8)=2f(4)=0;
令
| 1 |
| 2 |
∴f(2x)=2-2x,
又f(2x)=2f(x),
∴当
| 1 |
| 2 |
令
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
又f(2x)=2f(x),
∴当
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
令
| 1 |
| 8 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
又f(2x)=2f(x),
∴当
| 1 |
| 8 |
| 1 |
| 4 |
| 1 |
| 4 |
同理可得:当
| 1 |
| 16 |
| 1 |
| 8 |
| 1 |
| 8 |
令f(x)=
| 1 |
| 5 |
| 1 |
| 5 |
| 9 |
| 5 |
由1-x=
| 1 |
| 5 |
| 4 |
| 5 |
由
| 1 |
| 2 |
| 1 |
| 5 |
| 3 |
| 10 |
由
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 20 |
| 1 |
| 8 |
| 1 |
| 4 |
由
| 1 |
| 8 |
| 1 |
| 5 |
可推出以下都小于0.
∴方程f(x)=
| 1 |
| 5 |
| 3 |
| 10 |
故答案为:0,
| 3 |
| 10 |
点评:本题主要考查函数的解析式的求法,以及应用求自变量,注意运用赋值和转换的数学思想方法,同时解方程一定要注意自变量的范围.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
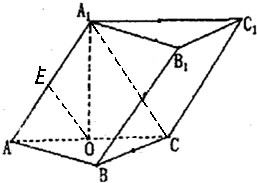 如图,三棱柱ABC-A1B1C1中,平面A1ACC1⊥平面ABC,△A1AC,△ABC均为正三角形,点O,E分别为AC,AA1中点.求二面角C1-AB-C的余弦值.
如图,三棱柱ABC-A1B1C1中,平面A1ACC1⊥平面ABC,△A1AC,△ABC均为正三角形,点O,E分别为AC,AA1中点.求二面角C1-AB-C的余弦值.