题目内容
已知单调递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2与a4的等差中项.
(1)求数列{an}的通项公式;
(2)若Tn=na1+(n-1)a2+…+2an-1+an,求Tn.
(1)求数列{an}的通项公式;
(2)若Tn=na1+(n-1)a2+…+2an-1+an,求Tn.
考点:数列的求和,等比数列的通项公式
专题:等差数列与等比数列
分析:(1)由已知条件利用等比数列和通项公式和等差数列的性质求出首项和公比,由此能求出数列{an}的通项公式.
(2)由Tn=n•2+(n-1)•22+(n-2)•23+…+2•2n-1+2n,利用错位相减法能求出Tn.
(2)由Tn=n•2+(n-1)•22+(n-2)•23+…+2•2n-1+2n,利用错位相减法能求出Tn.
解答:
解:(1)∵单调递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2与a4的等差中项,
∴2(a3+2)=a2+a4,
代入a2+a3+a4=28,
解得a3=8,
∴a2+a4=20,
设首项为a1,公比为q,
∴
,
解得a1=2,q=2,或a1=32,q=
,
又{an}单调递增,∴q=2,a1=2,
∴an=2n.
(2)Tn=na1+(n-1)a2+…+2an-1+an
=n•2+(n-1)•22+(n-2)•23+…+2•2n-1+2n,①
2Tn=n•22+(n-1)•23+…+2•2n+2n+1,②
②-①得:Tn=-2n+22+23+…+2n+2n+1
=-2n+
=2n+2-2n-4.
∴2(a3+2)=a2+a4,
代入a2+a3+a4=28,
解得a3=8,
∴a2+a4=20,
设首项为a1,公比为q,
∴
|
解得a1=2,q=2,或a1=32,q=
| 1 |
| 2 |
又{an}单调递增,∴q=2,a1=2,
∴an=2n.
(2)Tn=na1+(n-1)a2+…+2an-1+an
=n•2+(n-1)•22+(n-2)•23+…+2•2n-1+2n,①
2Tn=n•22+(n-1)•23+…+2•2n+2n+1,②
②-①得:Tn=-2n+22+23+…+2n+2n+1
=-2n+
| 22(1-2n) |
| 1-2 |
=2n+2-2n-4.
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,是中档题,解题时要注意错位相减法的合理运用.

练习册系列答案
相关题目
已知函数f(x)是R上的可导函数,f(x)的导数f′(x)的图象如图,则下列结论正确的是( )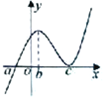

| A、a,c分别是极大值点和极小值点 |
| B、b,c分别是极大值点和极小值点 |
| C、f(x)在区间(a,c)上是增函数 |
| D、f(x)在区间(b,c)上是减函数 |
 如图所示,图中有5组数据,去掉
如图所示,图中有5组数据,去掉