题目内容
已知函数f（x）是R上的可导函数，f（x）的导数f′（x）的图象如图，则下列结论正确的是（ ）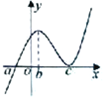
| A、a，c分别是极大值点和极小值点 |
| B、b，c分别是极大值点和极小值点 |
| C、f（x）在区间（a，c）上是增函数 |
| D、f（x）在区间（b，c）上是减函数 |
考点：利用导数研究函数的单调性
专题：数形结合,函数的性质及应用,导数的综合应用
分析：由极值点的定义，即在导数为0的根的附近，考虑导数的符号，左负右正，为极小值点，左正右负，为极大值点，再由单调性的判断，导数大于0，即为增区间，小于0，即为减区间．即可判断A，B，D错，C对．
解答：
解：对于A，在x=a处导数左负右正，为极小值点，在x=c处导数左正右正，不为极值点，故A错；
对于B，在x=b处导数不为0，在x=c处导数左正右正，不为极值点，故B错；
对于C，f（x）在区间（a，c）上的导数大于0，则f（x）在区间（a，c）上是增函数，故C对；
对于D，f（x）在区间（b，c）上的导数大于0，则f（x）在区间（b，c）上是增函数，故D错．
故选C．
解：对于A，在x=a处导数左负右正，为极小值点，在x=c处导数左正右正，不为极值点，故A错；对于B，在x=b处导数不为0，在x=c处导数左正右正，不为极值点，故B错；
对于C，f（x）在区间（a，c）上的导数大于0，则f（x）在区间（a，c）上是增函数，故C对；
对于D，f（x）在区间（b，c）上的导数大于0，则f（x）在区间（b，c）上是增函数，故D错．
故选C．
点评：本题考查了利用导函数的图象研究函数的单调性、极值等性质，属于中档题．
练习册系列答案
备战中考寒假系列答案
相关题目
设球的半径R=
cm，则此球的表面积为（ ）
| 3 |
| A、36πcm2 | ||
| B、12πcm2 | ||
C、4
| ||
| D、4πcm2 |
在△ABC中，若a=3，cosA=-
，则△ABC的外接圆的直径为（ ）
| 1 |
| 2 |
A、
| ||||
B、2
| ||||
C、
| ||||
D、
|
将函数y=sin（x+
）的图象向右平移 π个单位后，所得的函数图象（ ）
| π |
| 6 |
A、关于点(-
| ||
B、关于直线x=
| ||
C、关于点(
| ||
D、关于直线x=
|
