题目内容
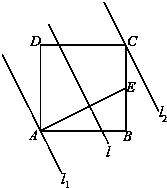 如图正方形ABCD边长为4cm,E为BC的中点,现用一条垂直于AE的直线l以0.4m/s的速度从l1平行移动到l2,则在t秒时直线l扫过的正方形ABCD的面积记为F(t)(m2),则F(t)的函数图象大概是( )
如图正方形ABCD边长为4cm,E为BC的中点,现用一条垂直于AE的直线l以0.4m/s的速度从l1平行移动到l2,则在t秒时直线l扫过的正方形ABCD的面积记为F(t)(m2),则F(t)的函数图象大概是( )A、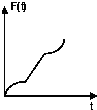 |
B、 |
C、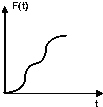 |
D、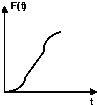 |
考点:函数的图象与图象变化
专题:函数的性质及应用
分析:分析出l与正方形AD边有交点时和l与正方形CD边有交点时,函数图象的凸凹性,进而利用排除法可得答案.
解答:
解:当l与正方形AD边有交点时,
此时直线l扫过的正方形ABCD的面积随t的增大而增大的速度加快,故此段为凹函数,可排除A,B,
当l与正方形CD边有交点时,
此时直线l扫过的正方形ABCD的面积随t的增大而增大的速度不变,故此段为一次函数,图象就在为直线,可排除C,
故选:D
此时直线l扫过的正方形ABCD的面积随t的增大而增大的速度加快,故此段为凹函数,可排除A,B,
当l与正方形CD边有交点时,
此时直线l扫过的正方形ABCD的面积随t的增大而增大的速度不变,故此段为一次函数,图象就在为直线,可排除C,
故选:D
点评:本题考查的知识点是函数的图象与图象变化,其中分析出函数图象的凸凹性是解答的关键.

练习册系列答案
相关题目
下列函数中最小值为4的是( )
| A、y=4ex+e-x | ||||
B、y=x+
| ||||
C、y=
| ||||
| D、y=log3x+logx3(0<x<1) |
f(a)=a3-2a+1,求f(2)=( )
| A、3 | B、4 | C、5 | D、2 |
执行所示的程序框图,若输出的S是2047,则判断框内应填写( )


| A、n≤9? | B、n≤10? |
| C、n≥10? | D、n≥11? |
在△ABC中,若AD是边BC上的高,且AD=BC,则
+
的最大值是( )
| AC |
| AB |
| AB |
| AC |
| A、2 | ||
B、
| ||
C、
| ||
| D、3 |
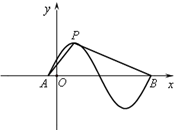 函数y=sin(ωx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,若cos∠APB=-
函数y=sin(ωx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,若cos∠APB=-