题目内容
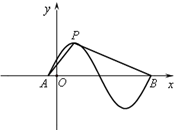 函数y=sin(ωx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,若cos∠APB=-
函数y=sin(ωx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,若cos∠APB=-
| ||
| 5 |
A、
| ||
B、
| ||
C、
| ||
| D、π |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由解析式求出函数的周期与最值,做出辅助线过p作PD⊥x轴于D,根据周期的大小看出直角三角形中直角边的长度,解出∠APD与∠BPD的正弦、余弦函数值,利用cos∠APB=-
,求出ω的值.
| ||
| 5 |
解答:
解:函数y=sin(ωx+φ)
∴AB=T=
,最大值为1,
过P作PD⊥x轴于D,则AD是四分之一个周期,有AD=
,DB=
,DP=1,
∴AP=
,BP=
在直角三角形ADP中有cos∠APD=
,sin∠APD=
,
在直角三角形BDP中cos∠BPD=
,sin∠BPD=
.
cos∠APB=cos(∠APD+∠BPD)=
•
-
•
=-
.
∴
-
=-
,
化简得:64ω4-160π2ω2+36π4=0,解得ω=
.
故选:B.
∴AB=T=
| 2π |
| ω |
过P作PD⊥x轴于D,则AD是四分之一个周期,有AD=
| π |
| 2ω |
| 3π |
| 2ω |
∴AP=
1+
|
1+
|
在直角三角形ADP中有cos∠APD=
| DP |
| AP |
| AD |
| AP |
在直角三角形BDP中cos∠BPD=
| DP |
| BP |
| BD |
| BP |
cos∠APB=cos(∠APD+∠BPD)=
| DP |
| AP |
| DP |
| BP |
| AD |
| AP |
| BD |
| BP |
| ||
| 5 |
∴
| 1 | ||||||||
|
| ||||||||
|
| ||
| 5 |
化简得:64ω4-160π2ω2+36π4=0,解得ω=
| π |
| 2 |
故选:B.
点评:本题考查三角函数的图象的应用与两角和的余弦函数公式的应用,本题解题的关键是看出函数的周期,把要求正弦的角放到直角三角形中,利用三角函数的定义得到结果,本题是一个中档题目.

练习册系列答案
相关题目
以下命题:
①任意向量
2,有
2=|
|2成立;
②存在复数z,有z2=|z|2成立
③若ξ~B(4,0.25),则Dξ=1;
④如果命题p是真命题,命题q是假命题,则命题“p且q”是真命题
其中正确命题的个数为( )
①任意向量
| a |
| a |
| a |
②存在复数z,有z2=|z|2成立
③若ξ~B(4,0.25),则Dξ=1;
④如果命题p是真命题,命题q是假命题,则命题“p且q”是真命题
其中正确命题的个数为( )
| A、1 | B、2 | C、3 | D、4 |
已知函数f(x)=ex-1,g(x+1)=-x2+2x,若f(a)=g(b),则b的取值范围是( )
A、[2-
| ||||
B、(2-
| ||||
| C、[1,3] | ||||
| D、(1,3) |
设变量x,y满足约束条件
,则z=x-3y的最大值为( )
|
| A、-4 | B、4 | C、3 | D、-3 |
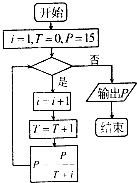 一个算法的程序框图如图所示,若该程序输出的P位于区间(10-4,10-3)内,则判断框内应填入的条件是( )
一个算法的程序框图如图所示,若该程序输出的P位于区间(10-4,10-3)内,则判断框内应填入的条件是( )| A、T≤3 | B、T≤4 |
| C、T≤5 | D、T≤6 |
已知全集U=R,集合A={x|x<3},B={x|x>2},则图中阴影部分表示的集合为( )


| A、(4,+∞) |
| B、(-∞,3) |
| C、(-∞,2) |
| D、(2,3) |
函数y=2sin(2x+
)的最小正周期为( )
| π |
| 3 |
| A、4π | ||
| B、π | ||
| C、2π | ||
D、
|
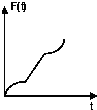
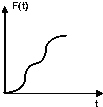
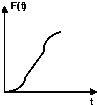
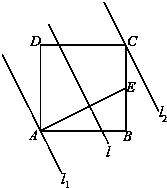 如图正方形ABCD边长为4cm,E为BC的中点,现用一条垂直于AE的直线l以0.4m/s的速度从l1平行移动到l2,则在t秒时直线l扫过的正方形ABCD的面积记为F(t)(m2),则F(t)的函数图象大概是( )
如图正方形ABCD边长为4cm,E为BC的中点,现用一条垂直于AE的直线l以0.4m/s的速度从l1平行移动到l2,则在t秒时直线l扫过的正方形ABCD的面积记为F(t)(m2),则F(t)的函数图象大概是( )