题目内容
在△ABC中,若AD是边BC上的高,且AD=BC,则
+
的最大值是( )
| AC |
| AB |
| AB |
| AC |
| A、2 | ||
B、
| ||
C、
| ||
| D、3 |
考点:解三角形
专题:计算题,解三角形
分析:利用AD是边BC上的高,且AD=BC,由面积关系得a2=bcsinA①,由余弦定理得a2=b2+c2-2bccosA②,将①代入②,再化简,利用辅助角公式,即可求出
+
的最大值.
| AC |
| AB |
| AB |
| AC |
解答:
解:∵AD是边BC上的高,且AD=BC,
∴由面积关系得a2=bcsinA①
由余弦定理得a2=b2+c2-2bccosA②
将①代入②得bc(sinA+2cosA)=b2+c2
即
+
=
+
=sinA+2cosA=
sin(A+α)≤
,其中tanα=2,
因此
+
的最大值是
.
故选:B.
∴由面积关系得a2=bcsinA①
由余弦定理得a2=b2+c2-2bccosA②
将①代入②得bc(sinA+2cosA)=b2+c2
即
| AC |
| AB |
| AB |
| AC |
| b |
| c |
| c |
| b |
| 5 |
| 5 |
因此
| AC |
| AB |
| AB |
| AC |
| 5 |
故选:B.
点评:本题考查三角形的面积公式,考查余弦定理,考查三角函数知识,考查系数分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知实数x、y满足
,则z=x+y的最小值等于( )
|
| A、0 | B、1 | C、4 | D、5 |
函数y=2sin(2x+
)的最小正周期为( )
| π |
| 3 |
| A、4π | ||
| B、π | ||
| C、2π | ||
D、
|
设{an}是一个等比数列,它的前3项的和为10,前6项的和为30,则它的前9项的和为( )
| A、50 | B、60 | C、70 | D、90 |
若集合A={x||x|≤1},B={y|y=2x,x∈R},A∩B=( )
| A、∅ |
| B、{x|0≤x≤1} |
| C、{x|-1≤x≤1} |
| D、{x|0<x≤1} |
已知△ABC的三个内角A,B,C所对的边分别为a,b,c,若b-a=c-b=1且C=2A,则cosC=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
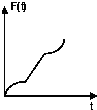
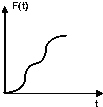
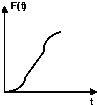
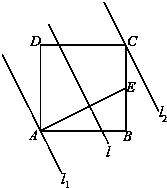 如图正方形ABCD边长为4cm,E为BC的中点,现用一条垂直于AE的直线l以0.4m/s的速度从l1平行移动到l2,则在t秒时直线l扫过的正方形ABCD的面积记为F(t)(m2),则F(t)的函数图象大概是( )
如图正方形ABCD边长为4cm,E为BC的中点,现用一条垂直于AE的直线l以0.4m/s的速度从l1平行移动到l2,则在t秒时直线l扫过的正方形ABCD的面积记为F(t)(m2),则F(t)的函数图象大概是( )