题目内容
某高中有甲乙等5名同学被一所大学自主招生录取后，大学提供了4个学院给这5名学生选择．假设选择每个学院是等可能的，则这5人中甲乙进同一学院，且每所学院都有学生选择的概率是 ．
考点：古典概型及其概率计算公式
专题：概率与统计
分析：利用分类计数原理求出所有的就读方式，再利用捆绑法求出仅有两名学生录取到同一所大学的就读方法，利用古典概型概率公式求出概率．
解答：
解：五位同学到4个学院就读的所有就读方式有45，
则这5人中甲乙进同一学院，就读方式有A44=24，
则这5人中甲乙进同一学院，且每所学院都有学生选择的概率是P=
=
故答案为：
．
则这5人中甲乙进同一学院，就读方式有A44=24，
则这5人中甲乙进同一学院，且每所学院都有学生选择的概率是P=
| 24 |
| 45 |
| 3 |
| 128 |
故答案为：
| 3 |
| 128 |
点评：本题考查利用分类计数原理及排列组合公式求完成事件的方法数；利用古典概型概率公式求事件的概率．
练习册系列答案
相关题目
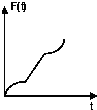
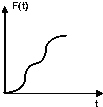
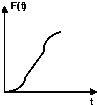
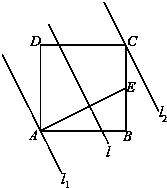如图正方形ABCD边长为4cm，E为BC的中点，现用一条垂直于AE的直线l以0.4m/s的速度从l1平行移动到l2，则在t秒时直线l扫过的正方形ABCD的面积记为F（t）（m2），则F（t）的函数图象大概是（ ）
