题目内容
已知点P在△ABC内（包括边界），且
=λ
+μ
，若对于满足条件的λ和μ，都有|aλ+bμ|≤2成立，则动点Q（a，b）形成的平面区域的面积（ ）
| AP |
| AB |
| AC |
| A、8 | B、16 | C、32 | D、64 |
考点：二元一次不等式（组）与平面区域,平面向量的基本定理及其意义
专题：不等式的解法及应用
分析：通过已知的向量关系以及三角形与P的位置，确定λ，μ的关系，得到可行域，然后利用表达式的几何意义，求出表达式的最大值．
解答：
解答：解：因为三角形ABC内一点，且
=λ
+μ
，
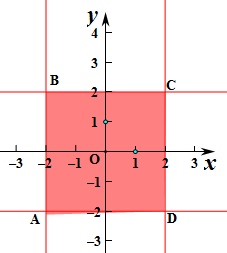
当p点在BC上时，λ+μ=1，
当P在三角形ABC内．
∴0≤λ+μ≤1
0≤λ≤1，0≤μ≤1，
要使|aλ+bμ|≤2成立，
则当λ=0，μ=1时，或μ=0，λ=1时不等式恒成立，
即
，
则动点Q（a，b）对应的平面区域为矩形，
∴矩形的面积为4×4=16．
故选：B
| AP |
| AB |
| AC |
当p点在BC上时，λ+μ=1，
当P在三角形ABC内．
∴0≤λ+μ≤1
0≤λ≤1，0≤μ≤1，
要使|aλ+bμ|≤2成立，
则当λ=0，μ=1时，或μ=0，λ=1时不等式恒成立，
即
|
则动点Q（a，b）对应的平面区域为矩形，
∴矩形的面积为4×4=16．
故选：B
点评：本题以向量为载体，考查线性规划的简单应用，抽象出约束条件是解题的关键，考查转化思想以及计算能力．
练习册系列答案
相关题目
以下命题：
①任意向量
2，有
2=|
|2成立；
②存在复数z，有z2=|z|2成立
③若ξ～B（4，0.25），则Dξ=1；
④如果命题p是真命题，命题q是假命题，则命题“p且q”是真命题
其中正确命题的个数为（ ）
①任意向量
| a |
| a |
| a |
②存在复数z，有z2=|z|2成立
③若ξ～B（4，0.25），则Dξ=1；
④如果命题p是真命题，命题q是假命题，则命题“p且q”是真命题
其中正确命题的个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
设复数z1=1-i，z2=x+2i（x∈R），若
为实数，则x=（ ）
| z2 |
| z1 |
| A、-2 | B、-1 | C、1 | D、2 |
已知函数f（x）=ex-1，g（x+1）=-x2+2x，若f（a）=g（b），则b的取值范围是（ ）
A、[2-
| ||||
B、（2-
| ||||
| C、[1，3] | ||||
| D、（1，3） |
设变量x，y满足约束条件
，则z=x-3y的最大值为（ ）
|
| A、-4 | B、4 | C、3 | D、-3 |
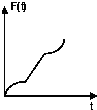
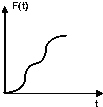
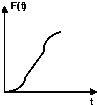
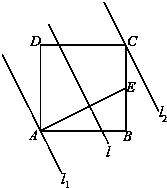如图正方形ABCD边长为4cm，E为BC的中点，现用一条垂直于AE的直线l以0.4m/s的速度从l1平行移动到l2，则在t秒时直线l扫过的正方形ABCD的面积记为F（t）（m2），则F（t）的函数图象大概是（ ）
已知实数x、y满足
，则z=x+y的最小值等于（ ）
|
| A、0 | B、1 | C、4 | D、5 |