题目内容
f(a)=a3-2a+1,求f(2)=( )
| A、3 | B、4 | C、5 | D、2 |
考点:函数的值
专题:计算题,函数的性质及应用
分析:直接利用函数的表达式求出函数的值即可.
解答:
解:∵f(a)=a3-2a+1,
∴f(2)=23-22+1=5.
故选:C.
∴f(2)=23-22+1=5.
故选:C.
点评:本题考查函数值的求法,考查计算能力.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
已知函数f(x)=ex-1,g(x+1)=-x2+2x,若f(a)=g(b),则b的取值范围是( )
A、[2-
| ||||
B、(2-
| ||||
| C、[1,3] | ||||
| D、(1,3) |
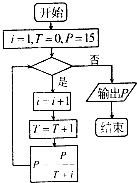 一个算法的程序框图如图所示,若该程序输出的P位于区间(10-4,10-3)内,则判断框内应填入的条件是( )
一个算法的程序框图如图所示,若该程序输出的P位于区间(10-4,10-3)内,则判断框内应填入的条件是( )| A、T≤3 | B、T≤4 |
| C、T≤5 | D、T≤6 |
执行如图的程序框图,若输出的S是255,则判断框内应填写( )


| A、n≤6? | B、n≤7? |
| C、n≥7? | D、n≥8? |
已知全集U=R,集合A={x|x<3},B={x|x>2},则图中阴影部分表示的集合为( )


| A、(4,+∞) |
| B、(-∞,3) |
| C、(-∞,2) |
| D、(2,3) |
已知圆C:x2+y2=2与直线l:x+y+
=0,则圆C被直线l所截得的弦长为( )
| 2 |
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
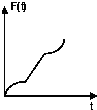
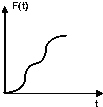
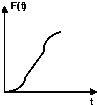
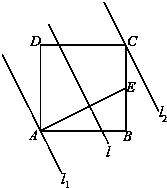 如图正方形ABCD边长为4cm,E为BC的中点,现用一条垂直于AE的直线l以0.4m/s的速度从l1平行移动到l2,则在t秒时直线l扫过的正方形ABCD的面积记为F(t)(m2),则F(t)的函数图象大概是( )
如图正方形ABCD边长为4cm,E为BC的中点,现用一条垂直于AE的直线l以0.4m/s的速度从l1平行移动到l2,则在t秒时直线l扫过的正方形ABCD的面积记为F(t)(m2),则F(t)的函数图象大概是( )