题目内容
{(x,y)|0≤x≤1,-1≤y≤1}中任取一点,恰好在y2=x和x=1围成区域的概率 .
考点:几何概型
专题:计算题,概率与统计
分析:(x,y)|0≤x≤1,-1≤y≤1}的面积为2,y2=x和x=1围成区域的面积为2
dx=
x
=
,即可求出概率.
| ∫ | 1 0 |
| x |
| 2 |
| 3 |
| 3 |
| 2 |
| | | 1 0 |
| 2 |
| 3 |
解答:
解:{(x,y)|0≤x≤1,-1≤y≤1}的面积为2,y2=x和x=1围成区域的面积为2
dx=
x
=
,
∴所求的概率为
=
.
故答案为:
.
| ∫ | 1 0 |
| x |
| 2 |
| 3 |
| 3 |
| 2 |
| | | 1 0 |
| 2 |
| 3 |
∴所求的概率为
| ||
| 2 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查几何概型,考查学生的计算能力,确定y2=x和x=1围成区域的面积是关键.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
某化工厂单位要在600名员工中抽取60名员工调查职工身体健康状况,其中青年员工300名,中年员工200名,老年员工100名,下列说法错误的是( )
| A、老年人应作为重点调查对象,故老年人应该抽超过30名 | ||
B、每个人被抽到的概率相同为
| ||
| C、应使用分层抽样抽取样本调查 | ||
| D、抽出的样本能在一定程度上反应总体的健康状况 |
设函数f(x)=x2+2ax+b2,若a∈[0,2],b∈[0,3],则函数f(x)有零点的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
方程log2x+x-2=0的解所在的区间为( )
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
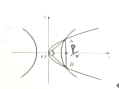 如图,双曲线
如图,双曲线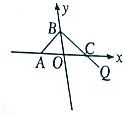 如图,已知A(-3p,0)(p>0),B,C两点分别在y轴和x轴上运动,并且满足
如图,已知A(-3p,0)(p>0),B,C两点分别在y轴和x轴上运动,并且满足