Question

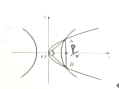如图，双曲线

x2

a2

-

y2

b2

=1的右焦点与抛物线y²=2px（p＞0）的焦点重合，它们的公共点A、B与坐标原点O构成等腰直角三角形，且焦点在直线AB上，则双曲线的离心率为

 

．

Answer 1

考点：双曲线的简单性质

专题：计算题,圆锥曲线的定义、性质与方程

分析：由对称性可得，OA=OB，O为直角顶点，由x=

p

2

代入抛物线方程，令x=c，代入双曲线方程，求得AB的长，再由a，b，c的关系和离心率公式，计算即可得到．

解答： 解：由对称性可得，OA=OB，O为直角顶点，
由x=

p

2

代入抛物线方程可得，y=±p，
则AB=2p，
又c=

p

2

，
令x=c，代入双曲线方程则有y=±

b2

a

，
则有AB=

2b2

a

，
即有2ac=b²=c²-a²，e=

c

a

，
则有e²-2e-1=0，解得e=1+

2

（负值舍去）．
故答案为：1+

2

．

点评：本题考查抛物线和双曲线的方程和性质，考查直线方程和圆锥曲线方程联立，求交点，考查运算能力，属于基础题．