Question

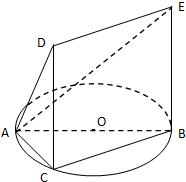如图，一简单组合体的一个面ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行四边形，且DC⊥平面ABC．
（1）证明：BC⊥平面ACD；
（2）若AB=2，BC=1，tan∠EAB=

3

2

，试求该简单组合体的体积V．

Answer 1

考点：直线与平面垂直的性质,棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：（1）由已知可得DC⊥BC，BC⊥AC且DC∩AC=C，从而有BC⊥平面ADC．
（2）解法1：所求简单组合体的体积：V=V_E-ABC+V_E-ADC，根据已知，可先求BE=

3

，AC=

AB2-BC2

=

3

，求得VE-ADC=

1

3

S△ADC•DE=

1

6

AC•DC•DE=

1

2

，
VE-ABC=

1

3

S△ABC•EB=

1

6

AC•BC•EB=

1

2

，从而可求该简单组合体的体积V．
解法2：将该简单组合体还原成一侧棱与底面垂直的三棱柱，可先求BE=

3

，AC=

AB2-BC2

=

3

，由V=V_ACB-FDE-V_E-ADF即可求该简单组合体的体积V．

解答： 解：（1）证明：
∵DC⊥平面ABC，BC?平面ABC∴DC⊥BC．----------------（2分）
∵AB是圆O的直径∴BC⊥AC且DC∩AC=C
∴BC⊥平面ADC．------------------------------------（5分）

（2）解法1：所求简单组合体的体积：V=V_E-ABC+V_E-ADC-----（7分）
∵AB=2，BC=1，tan∠EAB=

EB

AB

=

3

2

∴BE=

3

，AC=

AB2-BC2

=

3

-------------（9分）
∴VE-ADC=

1

3

S△ADC•DE=

1

6

AC•DC•DE=

1

2

-------（12分）
VE-ABC=

1

3

S△ABC•EB=

1

6

AC•BC•EB=

1

2

---------（13分）
∴该简单几何体的体积V=1-------------------------------（14分）
解法2：将该简单组合体还原成一侧棱与底面垂直的三棱柱---（7分）
如图∵AB=2，BC=1，tan∠EAB=

EB

AB

=

3

2

∴BE=

3

，AC=

AB2-BC2

=

3

-------------（10分）
∴V=V_ACB-FDE-V_E-ADF=S△ACB•DC-

1

3

S△ADC•DE------------（12分）
=

1

2

AC•CB•DC-

1

6

AC•DC•DE
=

1

2

×

3

×1×

3

-

1

6

×

3

×

3

×1=1-------------------（14分）

点评：本题主要考察了直线与平面垂直的性质，棱柱、棱锥、棱台的体积的解法，属于基本知识的考查．