题目内容
设函数f(x)=
(a>0,a≠1).
(1)若g(x)的图象与f(x)的图象关于直线y轴对称,试求g(x)表达式;
(2)求证:g(x)+g(1-x)=1;
(3)计算g(
)+g(
)+g(
)+…+g(
)的值.
| 1 | ||
1+
|
(1)若g(x)的图象与f(x)的图象关于直线y轴对称,试求g(x)表达式;
(2)求证:g(x)+g(1-x)=1;
(3)计算g(
| 1 |
| 11 |
| 2 |
| 11 |
| 3 |
| 11 |
| 10 |
| 11 |
考点:函数的图象与图象变化,函数的值
专题:函数的性质及应用
分析:(1)根据对称的规律g(x)的图象与f(x)的图象关于直线y轴对称,g(x)=f(-x)求解即可.
(2)求出g(x)=
,g(1-x)=
=
=
,即可证明.
(3)运用g(x)+g(1-x)=1;整体求解即可.
(2)求出g(x)=
| ax | ||
ax+
|
| a1-x | ||
a1-x+
|
| a | ||
a+
|
| ||
|
(3)运用g(x)+g(1-x)=1;整体求解即可.
解答:
解:(1)f(x)=
(a>0,a≠1).
∵g(x)的图象与f(x)的图象关于直线y轴对称,
∴g(x)=f(-x)=
=
,
(2)∵g(x)=
,g(1-x)=
=
=
,
∴g(x)+g(1-x)=
+
=1,
即g(x)+g(1-x)=1,
(3)∵g(x)+g(1-x)=1,
∴g(
)+g(
)+g(
)+…+g(
)=5.
| 1 | ||
1+
|
∵g(x)的图象与f(x)的图象关于直线y轴对称,
∴g(x)=f(-x)=
| 1 | ||
1+
|
| ax | ||
ax+
|
(2)∵g(x)=
| ax | ||
ax+
|
| a1-x | ||
a1-x+
|
| a | ||
a+
|
| ||
|
∴g(x)+g(1-x)=
| ax | ||
ax+
|
| ||
|
即g(x)+g(1-x)=1,
(3)∵g(x)+g(1-x)=1,
∴g(
| 1 |
| 11 |
| 2 |
| 11 |
| 3 |
| 11 |
| 10 |
| 11 |
点评:本题综合考查了函数的定义,性质,属于综合题,但是难度不大,属于容易题.

练习册系列答案
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
已知等比数列{an}满足an>0,n=1,2,…,且a5•a2n-5=22n(n≥3),则当n≥1时,log2a1+log2a3+…+log2a2n-1=( )
| A、n(2n-1) |
| B、(n+1)2 |
| C、n2 |
| D、(n-1)2 |
已知函数f(x)=
,若f(m)<1,则m的取值范围是( )
|
| A、(-1,1) |
| B、(-∞,1) |
| C、(-1,0] |
| D、(0,1) |
目标函数Z=2x+y,变量x,y满足
,则有( )
|
| A、Zmax=12,Zmin=3 |
| B、Zmax=12,Z无最小值 |
| C、Zmin=3,Z无最大值 |
| D、Z既无最大值,也无最小值 |
计算:
(sinx+1)dx=( )
| ∫ | 2015 -2015 |
| A、-2015 | B、2015 |
| C、4030 | D、-4030 |
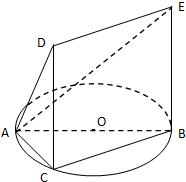 如图,一简单组合体的一个面ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.
如图,一简单组合体的一个面ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.