题目内容
已知向量
=(1，2)，
=(k+1，1)，若
⊥
，则k=（ ）
| a |
| b |
| a |
| b |
| A、3 | B、-3 | C、2 | D、-2 |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：运用向量垂直的条件：数量积为0，计算即可得到k．
解答：
解：向量
=(1，2)，
=(k+1，1)，
若
⊥
，则
•
=0，
即有k+1+2=0，
解得，k=-3．
故选B．
| a |
| b |
若
| a |
| b |
| a |
| b |
即有k+1+2=0，
解得，k=-3．
故选B．
点评：本题考查平面向量的垂直的条件：数量积为0，考查运算能力，属于基础题．
练习册系列答案
相关题目
已知等比数列{an}满足an＞0，n=1，2，…，且a5•a2n-5=22n（n≥3），则当n≥1时，log2a1+log2a3+…+log2a2n-1=（ ）
| A、n（2n-1） |
| B、（n+1）2 |
| C、n2 |
| D、（n-1）2 |
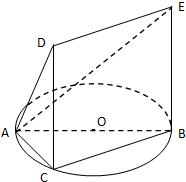如图，一简单组合体的一个面ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行四边形，且DC⊥平面ABC．