题目内容
已知函数f(x)=2x2-mx+3,当x∈(-2,+∞)时是增函数,当x∈(-∞,-2)时是减函数,则f(1)=( )
| A、-3 | B、13 |
| C、7 | D、含有m的变量 |
考点:二次函数的性质
专题:函数的性质及应用
分析:根据题意得出x=-2,为对称轴,即-2=
,代入解析式即可完成答案.
| m |
| 4 |
解答:
解:∵函数f(x)=2x2-mx+3,
当x∈(-2,+∞)时是增函数,当x∈(-∞,-2)时是减函数,
∴x=-2,为对称轴,
即-2=
,
故;m=-8,
∴f(x)=2x2+8x+3,
∴f(1)=13,
故选:B
当x∈(-2,+∞)时是增函数,当x∈(-∞,-2)时是减函数,
∴x=-2,为对称轴,
即-2=
| m |
| 4 |
故;m=-8,
∴f(x)=2x2+8x+3,
∴f(1)=13,
故选:B
点评:本题考查了对二次函数的性质,难度不大,属于容易题,计算即可.

练习册系列答案
相关题目
甲乙二人同时从A地赶往B地,甲先骑自行车到中点后改为跑步,而乙则是先跑步,到中点后改为骑自行车,最后二人同时到达B地,甲乙两人骑自行车速度都大于各自跑步速度,又知甲骑自行车比乙骑自行车的速度快.若某人离开A地的距离S与所用时间t的函数用图象表示如下,则在下列给出的四个函数中
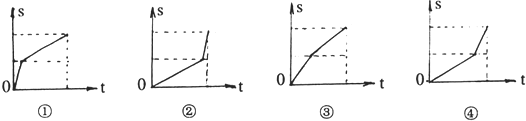
甲乙二人的图象只可能( )

甲乙二人的图象只可能( )
| A、甲是图①,乙是图② |
| B、甲是图①,乙是图④ |
| C、甲是图③,乙是图② |
| D、甲是图③,乙是图④ |
目标函数Z=2x+y,变量x,y满足
,则有( )
|
| A、Zmax=12,Zmin=3 |
| B、Zmax=12,Z无最小值 |
| C、Zmin=3,Z无最大值 |
| D、Z既无最大值,也无最小值 |
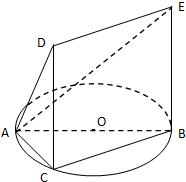 如图,一简单组合体的一个面ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.
如图,一简单组合体的一个面ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.