题目内容
古希腊人常用小石头在沙滩上摆成各种形状来研究数,如图:则第20个图共有 个黑点.


考点:归纳推理
专题:推理和证明
分析:根据已知中第1个图中黑点有1个,第2个图中黑点有1+2个,第3个图中黑点有1+2+3个,第4个图中黑点有1+2+3+4个,…归纳可得第n个图中黑点有1+2+3+…+n个,进而得到答案.
解答:
解:由已知中:
第1个图中黑点有1个,
第2个图中黑点有3=1+2个,
第3个图中黑点有6=1+2+3个,
第4个图中黑点有10=1+2+3+4个,
…
故第n个图中黑点有1+2+3+…+n=
个,
当n=20时,共有黑点210个,
故答案为:210
第1个图中黑点有1个,
第2个图中黑点有3=1+2个,
第3个图中黑点有6=1+2+3个,
第4个图中黑点有10=1+2+3+4个,
…
故第n个图中黑点有1+2+3+…+n=
| n(n+1) |
| 2 |
当n=20时,共有黑点210个,
故答案为:210
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列关于三个数log0.53,lnπ,(a2+3)0(a∈R)的大小关系,正确的是( )
| A、log0.53<(a2+3)0<lnπ |
| B、log0.53<lnπ<(a2+3)0 |
| C、(a2+3)0<log0.53<lnπ |
| D、lnπ<(a2+3)0<log0.53 |
计算:
(sinx+1)dx=( )
| ∫ | 2015 -2015 |
| A、-2015 | B、2015 |
| C、4030 | D、-4030 |
函数y=log2(2x-1)的定义域是( )
A、[
| ||
B、(
| ||
| C、(0,+∞) | ||
| D、(-∞,+∞) |
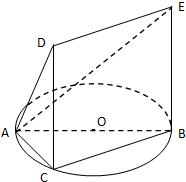 如图,一简单组合体的一个面ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.
如图,一简单组合体的一个面ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.