题目内容
下列说法中，正确的有 （把所有正确的序号都填上）．
①“?x∈R，使2x＞3”的否定是“?x∈R，使2x≤3”；
②函数y=sin（2x+
）sin（
-2x）的最小正周期是π；
③命题“函数f（x）在x=x0处有极值，则f′（x）=0”的否命题是真命题；
④函数f（x）=2x-x2的零点有2个．
①“?x∈R，使2x＞3”的否定是“?x∈R，使2x≤3”；
②函数y=sin（2x+
| π |
| 3 |
| π |
| 6 |
③命题“函数f（x）在x=x0处有极值，则f′（x）=0”的否命题是真命题；
④函数f（x）=2x-x2的零点有2个．
考点：命题的真假判断与应用
专题：简易逻辑
分析：写出原命题的否定，可判断①；利用诱导公式和倍角公式化简函数的解析式，进而求出周期可判断②；写出原命题的否命题，可判断③；确定函数f（x）=2x-x2的零点个数，可判断④．
解答：
解：对于①“?x∈R，使2x＞3“的否定是“?x∈R，使2x≤3”，满足特称命题的否定是全称命题的形式，所以①正确；
对于②，函数y=sin（2x+
）sin（
-2x）=
sin（4x+
），函数的最小正周期T=
=
，所以②不正确；
对于③，命题“函数f（x）在x=x0处有极值，则f'（x0）=0”的否命题是：若函数f（x）在x=x0处没极值，f'（x0）≠0，则显然不正确．例如f（x）=x3，x=0不是函数的极值点，但x=0时，导数为0，所以③不正确；
对于④，由题意可知：要研究函数f（x）=x2-2x的零点个数，只需研究函数y=2x，y=x2的图象交点个数即可．画出函数y=2x，y=x2的图象，
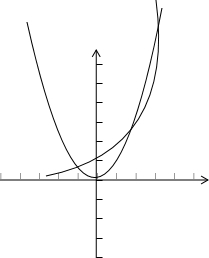
由图象可得有3个交点．所以④不正确；
故正确的命题只有：①，
故答案为：①
对于②，函数y=sin（2x+
| π |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
| 2π |
| 3 |
| 2π |
| 4 |
| π |
| 2 |
对于③，命题“函数f（x）在x=x0处有极值，则f'（x0）=0”的否命题是：若函数f（x）在x=x0处没极值，f'（x0）≠0，则显然不正确．例如f（x）=x3，x=0不是函数的极值点，但x=0时，导数为0，所以③不正确；
对于④，由题意可知：要研究函数f（x）=x2-2x的零点个数，只需研究函数y=2x，y=x2的图象交点个数即可．画出函数y=2x，y=x2的图象，
由图象可得有3个交点．所以④不正确；
故正确的命题只有：①，
故答案为：①
点评：本题考查了命题的真假判断与应用，考查了特称命题的否定，函数的周期性，取最值的条件，函数零点等知识点，难度中档．
练习册系列答案
相关题目
某市司法部门为了宣传《宪法》举办法律知识问答活动，随机对该市18～68岁的人群抽取一个容量为n的样本，并将样本数据分成五组：[18，28），[28，38），[38，48），[48，58），[58，68），再将其按从左到右的顺序分别编号为第1组，第2组，…，第5组，绘制了样本的频率分布直方图；并对回答问题情况进行统计后，结果如下表所示．已知函数f（x）定义域为[a，b]．则“函数f（x）在[a，b]上为单调函数”是“函数f（x）在[a，b]上有最大值和最小值”的（ ）
| A、充分但非必要条件 |
| B、必要但非充分条件 |
| C、充要条件 |
| D、既非充分也非必要条件 |
已知f（x）=sin（x+
），g（x）=cos（x-
），则下列结论正确的是（ ）
| π |
| 2 |
| π |
| 2 |
| A、函数y=f（x）•g（x）的最大值为1 | ||||
B、函数y=f（x）•g（x）的对称中心是（
| ||||
C、将f（x）的图象向右平移
| ||||
D、当x∈[-
|
若正实数a，b，c满足a+b+c=1，则
+
的最小值为（ ）
| 4 |
| a+1 |
| 1 |
| b+c |
A、
| ||
| B、2 | ||
C、
| ||
| D、4 |