题目内容
已知数列{an}满足a1=1,且an=2an-1+2n(n≥2且n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{an}的前n项和为Sn,求Sn;
(Ⅲ)设bn=
,试求数列{bn}的最大项.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{an}的前n项和为Sn,求Sn;
(Ⅲ)设bn=
| Sn-3 |
| 3n |
考点:数列递推式,数列的函数特性,数列的求和
专题:点列、递归数列与数学归纳法
分析:(Ⅰ)根据数列的递推关系即可求数列{an}的通项公式;
(Ⅱ)利用错位相减法即可求数列{an}的前n项和为Sn;
(Ⅲ)求出bn=
的通项公式,建立不等式关系即可试求数列{bn}的最大项.
(Ⅱ)利用错位相减法即可求数列{an}的前n项和为Sn;
(Ⅲ)求出bn=
| Sn-3 |
| 3n |
解答:
解:(Ⅰ)由an=2an-1+2n(n≥2且n∈N*).
得
=
+1,
即{
}是首项为
,公差d=1的等差数列,
则
=
+(n-1)=n-
,
数列{an}的通项公式an=(2n-1)•2n-1;
(Ⅱ)设数列{an}的前n项和为Sn,求Sn;
∵an=(2n-1)•2n-1;
∴Sn=1•20+3•21+5•22+…+(2n-1)•2n-1;
2Sn=1•21+3•22+…+(2n-1)•2n;
两式相减得-Sn=1+2(21+22+…+2n-1-(2n-1)•2n=1+
-(2n-1)•2n=-3+(3-2n)•2n;
∴Sn=(2n-3)•2n+3
(Ⅲ)∵bn=
,∴bn═(2n-3)•(
)n,
由
,
即
,
解得
≤n≤
,即n=4,
即数列{bn}的最大项为b4=
.
得
| an |
| 2n |
| an-1 |
| 2n-1 |
即{
| an |
| 2n |
| 1 |
| 2 |
则
| an |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
数列{an}的通项公式an=(2n-1)•2n-1;
(Ⅱ)设数列{an}的前n项和为Sn,求Sn;
∵an=(2n-1)•2n-1;
∴Sn=1•20+3•21+5•22+…+(2n-1)•2n-1;
2Sn=1•21+3•22+…+(2n-1)•2n;
两式相减得-Sn=1+2(21+22+…+2n-1-(2n-1)•2n=1+
| 22(1-2n+1) |
| 1-2 |
∴Sn=(2n-3)•2n+3
(Ⅲ)∵bn=
| Sn-3 |
| 3n |
| 2 |
| 3 |
由
|
即
|
解得
| 7 |
| 2 |
| 9 |
| 2 |
即数列{bn}的最大项为b4=
| 80 |
| 81 |
点评:本题主要考查递递推数列的应用,综合考查学生的运算能力,要求熟练掌握求和的常见方法.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
已知数列{an}是等比数列,Sn是其前n项和,且a3=2,S3=6,则a5=( )
A、2或-
| ||
B、
| ||
| C、±2 | ||
D、2或
|
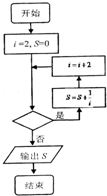
如图给出的是计算
+
+
+…+
的值的程序框图,其中判断框内应填入的是( )
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 2014 |

| A、i≤2013 |
| B、i≤2015 |
| C、i≤2017 |
| D、i≤2019 |
已知复数z1=2+ai(a∈R),z2=1-2i,若
为纯虚数,则|z1|=( )
| z1 |
| z2 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
已知i是虚数单位,若复数Z=a+bi(a,b∈R)在复平面内对应的点位于第四象限,则复数Z•i在复平面内对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知sin(π+α)=
,且α是第四象限角,则cos(α-2π)的值是( )
| 2 |
| 3 |
A、±
| ||||
B、
| ||||
C、±
| ||||
D、
|