题目内容
在△ABC中，设
=（2sinB，-
），
=（cos2B，1-2sin2
），且
∥
，cosC=
，求sin（B-A）的值．
| x |
| 3 |
| y |
| B |
| 2 |
| x |
| y |
| 3 |
| 10 |
考点：平面向量共线（平行）的坐标表示,两角和与差的正弦函数
专题：平面向量及应用
分析：利用向量共线定理、倍角公式、两角和差的正弦公式可得B，再利用同角三角函数基本关系式、两角和差的正弦公式、三角形的内角和定理即可得出．
解答：
解：∵
∥
，∴2sinB(1-2sin2
)+
cos2B=0，化为2sinBcosB+
cos2B=0，即sin2B+
cos2B=0．
∴sin(2B+
)=0，∵B∈（0，π），∴2B+
=π或2π，解得B=
或B=
．
∵cosC=
＜
，∴C＞
．因此B＜
．∴B=
舍去．
∴B=
．
∵cosC=
，∴sinC=
=
．
∴sin（B-A）=sin[
-(π-
-C)]=sin(C-
)=sinCcos
-cosCsin
=
×
-
×
=
．
| x |
| y |
| B |
| 2 |
| 3 |
| 3 |
| 3 |
∴sin(2B+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
∵cosC=
| 3 |
| 10 |
| 1 |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
| 5π |
| 6 |
∴B=
| π |
| 3 |
∵cosC=
| 3 |
| 10 |
| 1-cos2C |
| ||
| 10 |
∴sin（B-A）=sin[
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| ||
| 10 |
| ||
| 2 |
| 3 |
| 10 |
| ||||
| 20 |
点评：本题考查了向量共线定理、倍角公式、两角和差的正弦公式、同角三角函数基本关系式、三角形的内角和定理等基础知识与基本技能方法，考查了计算能力，属于中档题．
练习册系列答案
导学全程练创优训练系列答案
相关题目
有4条线段长度分别为3，5，7，9，从这4条线段中任取3条，则所取3条线段不能构成一个三角形的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设等比数列{an}的公比为q，若a8-a4=24，a5-a1=3，则实数q的值为（ ）
| A、3 | ||
| B、2 | ||
C、
| ||
D、
|
下列命题中，正确的是（ ）
| A、如果两条平行直线中的一条与平面α平行，那么另一条也与平面α平行 |
| B、若两个平面垂直，则一个平面内的任一条直线必垂直于另一个平面 |
| C、若直线l与平面α平行，则l与平面α内的任意一条直线都没有公共点 |
| D、垂直于同一平面的两个平面互相平行 |
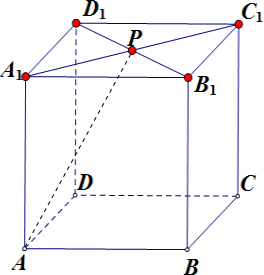在一个正方体ABCD-A1B1C1D1中，P为正方形A1B1C1D1的中心，求证AP⊥PB1．