题目内容
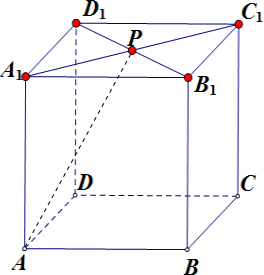在一个正方体ABCD-A1B1C1D1中，P为正方形A1B1C1D1的中心，求证AP⊥PB1．考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：如图所示，连接AB1，AD1．由正方体ABCD-A1B1C1D1可得：AB1=AD1，B1P=D1P．再利用等腰三角形的性质即可得出．
解答：
证明：如图所示，连接AB1，AD1．
由正方体ABCD-A1B1C1D1可得：AB1=AD1，B1P=D1P．
∴AP⊥PB1．
由正方体ABCD-A1B1C1D1可得：AB1=AD1，B1P=D1P．
∴AP⊥PB1．
点评：本题考查了正方体的性质、等腰三角形的性质，属于基础题．
练习册系列答案
相关题目
X大学2014年自主招生报名刚结束，某考生想知道这次报考的人数，他随机记录了50个考生的考号；已知考生的考号是从0001，0002，0003，…这样从小到大依次顺序排列．经计算，这50个考号的和是24966（其中0001+0002视为3），据此，估计2014年参加X大学自主招生的考生数约为（ ）
| A、500人 | B、1000人 |
| C、1500人 | D、2000人 |
函数f（x）=x-1的零点是（ ）
| A、0 | B、1 |
| C、（0，0） | D、（1，0） |