题目内容
y=
的对称中心是什么?画出其图象.
| x+3 |
| 2x+3 |
考点:函数的图象
专题:函数的性质及应用
分析:把原函数解析式变形得到y=
=
+
,即y-
=
,可设y′=y-
,x′=x+
得到y′=
为反比例函数且为奇函数,求出对称中心,然后画出图象即可.
| x+3 |
| 2x+3 |
| 1 |
| 2 |
| ||
x+
|
| 1 |
| 2 |
| ||
x+
|
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| x′ |
解答:
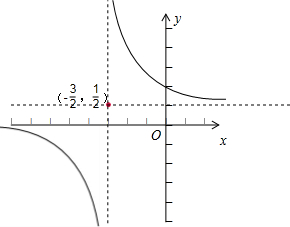 解:因为y=
解:因为y=
=
+
,即y-
=
,可设y′=y-
,x′=x+
得到y′=
为反比例函数且为奇函数,则对称中心为(0,0)即y′=0,x′=0得到y=
,x=-
,
所以函数y=
的对称中心为(-
,
).
图象如图:
 解:因为y=
解:因为y=| x+3 |
| 2x+3 |
| 1 |
| 2 |
| ||
x+
|
| 1 |
| 2 |
| ||
x+
|
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| x′ |
| 1 |
| 2 |
| 3 |
| 2 |
所以函数y=
| x+3 |
| 2x+3 |
| 3 |
| 2 |
| 1 |
| 2 |
图象如图:
点评:考查学生灵活运用奇偶函数图象对称性的能力.考查类比猜测,合情推理的探究能力和创新意识.

练习册系列答案
相关题目
阅读如图所示的程序框图,若输入的N=200,则输出的结果为( )


| A、101 | B、200 |
| C、100 | D、201 |
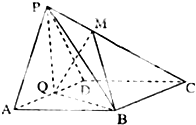 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD;
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD;