题目内容
3.若非零向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为锐角θ,且$\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|}$=cosθ,则称$\overrightarrow{a}$被$\overrightarrow{b}$“同余”.已知$\overrightarrow{b}$被$\overrightarrow{a}$“同余”,则$\overrightarrow{a}-\overrightarrow{b}$在$\overrightarrow{a}$上的投影是( )| A. | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{|\overrightarrow{a}|}$ | B. | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{{\overrightarrow{a}}^{2}}$ | C. | $\frac{{\overrightarrow{b}}^{2}-{\overrightarrow{a}}^{2}}{|\overrightarrow{b}|}$ | D. | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{|\overrightarrow{b}|}$ |
分析 根据“同余”的定义写出$\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}$=cosθ,再计算数量积($\overrightarrow{a}$-$\overrightarrow{b}$)$•\overrightarrow{a}$,从而求出$\overrightarrow{a}-\overrightarrow{b}$在$\overrightarrow{a}$上的投影.
解答 解:根据题意,$\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}$=cosθ,其中θ为$\overrightarrow{a}$、$\overrightarrow{b}$的夹角;
∴($\overrightarrow{a}$-$\overrightarrow{b}$)$•\overrightarrow{a}$=${\overrightarrow{a}}^{2}$-$\overrightarrow{a}$$•\overrightarrow{b}$=${\overrightarrow{a}}^{2}$-|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•$\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}$=${\overrightarrow{a}}^{2}$-${\overrightarrow{b}}^{2}$;
∴$\overrightarrow{a}-\overrightarrow{b}$在$\overrightarrow{a}$上的投影为:
|$\overrightarrow{a}$-$\overrightarrow{b}$|cos<$\overrightarrow{a}$-$\overrightarrow{b}$,$\overrightarrow{a}$>=|$\overrightarrow{a}$-$\overrightarrow{b}$|×$\frac{(\overrightarrow{a}-\overrightarrow{b})•\overrightarrow{a}}{|\overrightarrow{a}-\overrightarrow{b}|×|\overrightarrow{a}|}$=$\frac{{\overrightarrow{a}}^{2}{-\overrightarrow{b}}^{2}}{|\overrightarrow{a}|}$.
故选:A.
点评 本题考查了平面向量的数量积运算以及向量投影的计算问题,是基础题.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案| A. | -$\sqrt{3}$ | B. | -1 | C. | 1 | D. | $\sqrt{3}$ |
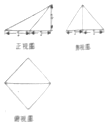
| A. | 3π | B. | 5π | C. | 10π | D. | 20π |
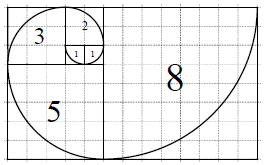 斐波那契数列{an}满足:${a_1}=1,{a_2}=1,{a_n}={a_{n-1}}+{a_{n-2}}({n≥3,n∈{N^*}})$.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前n项所占的格子的面积之和为Sn,每段螺旋线与其所在的正方形所围成的扇形面积为cn,则下列结论错误的是( )
斐波那契数列{an}满足:${a_1}=1,{a_2}=1,{a_n}={a_{n-1}}+{a_{n-2}}({n≥3,n∈{N^*}})$.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前n项所占的格子的面积之和为Sn,每段螺旋线与其所在的正方形所围成的扇形面积为cn,则下列结论错误的是( )| A. | ${S_{n+1}}=a_{n+1}^2+{a_{n+1}}•{a_n}$ | B. | a1+a2+a3+…+an=an+2-1 | ||
| C. | a1+a3+a5+…+a2n-1=a2n-1 | D. | 4(cn-cn-1)=πan-2•an+1 |
 某销售公司为了解员工的月工资水平,从1000位员工中随机抽取100位员工进行调查,得到如下的频率分布直方图:
某销售公司为了解员工的月工资水平,从1000位员工中随机抽取100位员工进行调查,得到如下的频率分布直方图: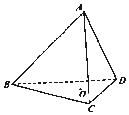 如图,在正四面体ABCD中,O是△BCD的中心,E,F分别是AB,AC上的动点,且$\overrightarrow{BE}$=λ$\overrightarrow{BA}$,$\overrightarrow{CF}$=(1-λ)$\overrightarrow{CA}$
如图,在正四面体ABCD中,O是△BCD的中心,E,F分别是AB,AC上的动点,且$\overrightarrow{BE}$=λ$\overrightarrow{BA}$,$\overrightarrow{CF}$=(1-λ)$\overrightarrow{CA}$