题目内容
18．一个几何体的三视图如所示，则该几何体的外接球表面积为（ ）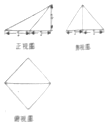
| A． | 3π | B． | 5π | C． | 10π | D． | 20π |
分析 由题意，直观图是以俯视图为底面，侧棱垂直与底面的四棱锥，求出该几何体的外接球的半径，可得结论．
解答 
解：由题意，直观图是以俯视图为底面，侧棱垂直与底面的四棱锥，
∴该几何体的外接球的半径为$\sqrt{1+4}$=$\sqrt{5}$，
∴该几何体的外接球表面积为4π•5=20π，
故选D．
点评 本题考查三视图，考查几何体的外接球表面积，求出几何体的外接球的半径是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．“2a＞2b＞1”是“$\root{3}{a}$＞$\root{3}{b}$”的（ ）条件．
| A． | 充要 | B． | 必要不充分 | ||
| C． | 充分不必要 | D． | 既不充分也不必要 |
9．欧拉公式eix=cosx+isinx（i是虚数单位，x∈R）是由瑞士著名的数学家欧拉发明的，它将指数函数的定义域扩大到复数，建立了三角函数与指数函数的关系，它在复变函数论里有及其重要的地位，被誉为“数学中的天桥”，根据欧拉公式，若$z={e^{\frac{π}{3}i}}$，则复数z2在复平面内所对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
3．若非零向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为锐角θ，且$\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|}$=cosθ，则称$\overrightarrow{a}$被$\overrightarrow{b}$“同余”．已知$\overrightarrow{b}$被$\overrightarrow{a}$“同余”，则$\overrightarrow{a}-\overrightarrow{b}$在$\overrightarrow{a}$上的投影是（ ）
| A． | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{|\overrightarrow{a}|}$ | B． | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{{\overrightarrow{a}}^{2}}$ | C． | $\frac{{\overrightarrow{b}}^{2}-{\overrightarrow{a}}^{2}}{|\overrightarrow{b}|}$ | D． | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{|\overrightarrow{b}|}$ |
7．已知F1，F2是椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左、右焦点，点P在椭圆C上，线段PF2与圆x2+y2=b2相切于点Q，且点Q为线段PF2的中点，则$\frac{{{a^2}+{e^2}}}{b}$（其中e为椭圆C的离心率）的最小值为（ ）
| A． | $\sqrt{6}$ | B． | $\frac{{3\sqrt{6}}}{4}$ | C． | $\sqrt{5}$ | D． | $\frac{{3\sqrt{5}}}{4}$ |