题目内容
15．
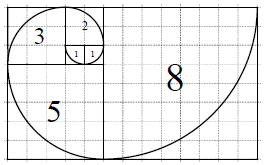斐波那契数列{an}满足：${a_1}=1，{a_2}=1，{a_n}={a_{n-1}}+{a_{n-2}}（{n≥3，n∈{N^*}}）$．若将数列的每一项按照下图方法放进格子里，每一小格子的边长为1，记前n项所占的格子的面积之和为Sn，每段螺旋线与其所在的正方形所围成的扇形面积为cn，则下列结论错误的是（ ）| A． | ${S_{n+1}}=a_{n+1}^2+{a_{n+1}}•{a_n}$ | B． | a1+a2+a3+…+an=an+2-1 | ||
| C． | a1+a3+a5+…+a2n-1=a2n-1 | D． | 4（cn-cn-1）=πan-2•an+1 |
分析 由题意，a1=1，a3=2，a4=3，a5=5，a6=8，a7=13，代入验证可得结论．
解答 解：由题意，a1=1，a3=2，a4=3，a5=5，a6=8，a7=13，
∴a1+a3=3≠a4-1，a1+a3+a5=8≠a6-1，
故选：C．
点评 本题考查归纳推理，考查学生的计算能力，正确计算是关键．
练习册系列答案
相关题目
3．若非零向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为锐角θ，且$\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|}$=cosθ，则称$\overrightarrow{a}$被$\overrightarrow{b}$“同余”．已知$\overrightarrow{b}$被$\overrightarrow{a}$“同余”，则$\overrightarrow{a}-\overrightarrow{b}$在$\overrightarrow{a}$上的投影是（ ）
| A． | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{|\overrightarrow{a}|}$ | B． | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{{\overrightarrow{a}}^{2}}$ | C． | $\frac{{\overrightarrow{b}}^{2}-{\overrightarrow{a}}^{2}}{|\overrightarrow{b}|}$ | D． | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{|\overrightarrow{b}|}$ |
20．已知i是虚数单位，则复数$\frac{-1+i}{3+4i}$的共轭复数在复平面内对应的点所在的象限为（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
7．已知F1，F2是椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左、右焦点，点P在椭圆C上，线段PF2与圆x2+y2=b2相切于点Q，且点Q为线段PF2的中点，则$\frac{{{a^2}+{e^2}}}{b}$（其中e为椭圆C的离心率）的最小值为（ ）
| A． | $\sqrt{6}$ | B． | $\frac{{3\sqrt{6}}}{4}$ | C． | $\sqrt{5}$ | D． | $\frac{{3\sqrt{5}}}{4}$ |
5．漳州水仙鳞茎硕大，箭多花繁，色美香郁，素雅娟丽，有“天下水仙数漳州”之美誉．现某水仙花雕刻师受雇每天雕刻250粒水仙花，雕刻师每雕刻一粒可赚1.2元，如果雕刻师当天超额完成任务，则超出的部分每粒赚1.7元；如果当天未能按量完成任务，则按实际完成的雕刻量领取当天工资．
（I）求雕刻师当天收入（单位：元）关于雕刻量n（单位：粒，n∈N）的函数解析式f（n）；
（Ⅱ）该雕刻师记录了过去10天每天的雕刻量n（单位：粒），整理得如表：
以10天记录的各雕刻量的频率作为各雕刻量发生的概率．
（ⅰ）求该雕刻师这10天的平均收入；
（ⅱ）求该雕刻师当天收入不低于300元的概率．
（I）求雕刻师当天收入（单位：元）关于雕刻量n（单位：粒，n∈N）的函数解析式f（n）；
（Ⅱ）该雕刻师记录了过去10天每天的雕刻量n（单位：粒），整理得如表：
| 雕刻量n | 210 | 230 | 250 | 270 | 300 |
| 频数 | 1 | 2 | 3 | 3 | 1 |
（ⅰ）求该雕刻师这10天的平均收入；
（ⅱ）求该雕刻师当天收入不低于300元的概率．