题目内容
14. 某销售公司为了解员工的月工资水平,从1000位员工中随机抽取100位员工进行调查,得到如下的频率分布直方图:
某销售公司为了解员工的月工资水平,从1000位员工中随机抽取100位员工进行调查,得到如下的频率分布直方图:(1)试由此图估计该公司员工的月平均工资;
(2)该公司工资发放是以员工的营销水平为重要依据来确定的,一般认为,工资低于4500元的员工属于学徒阶段,没有营销经验,若进行营销将会失败;高于4500元的员工是具备营销成熟员工,进行营销将会成功.现将该样本按照“学徒阶段工资”、“成熟员工工资”分为两层,进行分层抽样,从中抽出5人,在这5人中任选2人进行营销活动.活动中,每位员工若营销成功,将为公司赢得3万元,否则公司将损失1万元,试问在此次比赛中公司收入多少万元的可能性最大?
分析 (1)由频率分布直方图能估计该公司员工的月平均工资.
(2)抽取比为:$\frac{50}{100}=\frac{1}{20}$,从工资在[1500,4500)区间内抽2人,设这两位员工分别为1,2,从工资在[4500,7500]区间内抽3人,设这3人员工分别为A,B,C,从中任选2人,利用列举法能求出收入2万元的可能性最大.
解答 解:(1)由频率分布直方图估计该公司员工的月平均工资为:
0.01×10×20+0.01×10×30+0.02×10×40+0.03×10×50+0.02×10×60+0.01×10×70=4700(元).
(2)抽取比为:$\frac{50}{100}=\frac{1}{20}$,
从工资在[1500,4500)区间内抽100×(0.1+0.1+0.2)×$\frac{1}{20}$=2人,设这两位员工分别为1,2,
从工资在[4500,7500]区间内抽100×(0.3+0.2+0.1)×$\frac{1}{20}$=3人,设这3人员工分别为A,B,C,
从中任选2人,共有以下10种不同的等可能结果:
(1,2),(1,A),(1,B),(1,C),(2,A),(2,B),(2,C),(A,B),(A,C),(B,C),
两人营销都成功,公司收入6万元,有以下3种不同的等可能结果:(A,B),(A,C),(B,C),概率为$\frac{3}{10}$,
两人中有一人营销都成功,公司改入2万元,有6种结果:
(1,A),(1,B),(1,C),(2,A),(2,B),(2,C),概率为$\frac{3}{5}$,
两人营销都失败,公司损失2万元,有1种结果:(1,2),概率为$\frac{1}{10}$,
∵$\frac{1}{10}<\frac{3}{10}<\frac{3}{5}$,∴收入2万元的可能性最大.
点评 本题考查频率分布直方图的应用、概率的求法等基础知识,考查数据处理能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{|\overrightarrow{a}|}$ | B. | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{{\overrightarrow{a}}^{2}}$ | C. | $\frac{{\overrightarrow{b}}^{2}-{\overrightarrow{a}}^{2}}{|\overrightarrow{b}|}$ | D. | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{|\overrightarrow{b}|}$ |
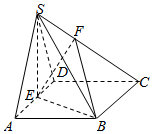 已知四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,SA=SD=$\sqrt{5},SB=\sqrt{7}$,点E是棱AD的中点,点F在棱SC上,且$\frac{SF}{SC}$=λ,SA∥平面BEF.
已知四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,SA=SD=$\sqrt{5},SB=\sqrt{7}$,点E是棱AD的中点,点F在棱SC上,且$\frac{SF}{SC}$=λ,SA∥平面BEF.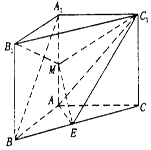 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.