题目内容
设函数fn(θ)＝sinnθ＋(－1)ncosnθ，0≤θ≤
，其中n为正整数．
(1)判断函数f1(θ)，f3(θ)的单调性，并就f1(θ)的情形证明你的结论；
(2)证明：2f6(θ)－f4(θ)＝(cos4θ－sin4θ)(cos2θ－sin2θ)．
解 (1)f1(θ)，f3(θ)在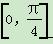
上均为单调递增函数．
对于函数f1(θ)＝sinθ－cosθ，设θ1<θ2，θ1，θ2∈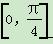，则f1(θ1)－f1(θ2)＝(sinθ1－sinθ2)＋(cosθ2－cosθ1)，
可得sinθ1<sinθ2，cosθ2<cosθ1，
∴f1(θ1)<f1(θ2)，函数f1(θ)在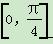上单调递增．
(2)证明：∵原式左边＝2(sin6θ＋cos6θ)－(sin4θ＋cos4θ)
＝2(sin2θ＋cos2θ)(sin4θ－sin2θ·cos2θ＋cos4θ)－(sin4θ＋cos4θ)
＝sin4θ－2sin2θcos2θ＋cos4θ＝(sin2θ－cos2θ)2＝cos22θ.
又∵原式右边＝(cos2θ－sin2θ)2＝cos22θ，
∴2f6(θ)－f4(θ)＝(cos4θ－sin4θ)(cos2θ－sin2θ)．
练习册系列答案
相关题目
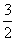an＋n－3.
＋
＋…＋
≥
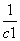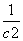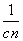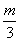都成立？若存在，求出m的值；若不存在，请说明理由．
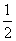×底×高；(3)三角形的中位线平行于第三边且等于第三边的
，且Sn＝n(2n－1)an，通过求a2，a3，a4，猜想an的表达式为( )
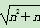<n＋1(n∈N*)，某同学用数学归纳法的证明过程如下：
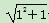<1＋1，不等式成立．
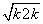<k＋1，则当n＝k＋1时，
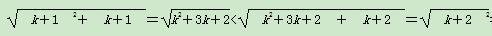＝(k＋1)＋1，
<loga