题目内容
已知数列{an}的前n项和为Sn满足:Sn=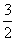 an+n-3.
an+n-3.
(1)求证:数列{an-1}是等比数列.
(2)令cn=log3(a1-1)+log3(a2-1)+…+log3(an-1),对任意n∈N*,是否存在正整数m,使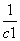 +
+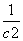 +…+
+…+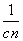 ≥
≥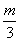 都成立?若存在,求出m的值;若不存在,请说明理由.
都成立?若存在,求出m的值;若不存在,请说明理由.
解 (1)证明:当n=1时,S1=a1=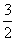 a1-2,解得a1=4.
a1-2,解得a1=4.
当n≥2时,由Sn=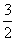 an+n-3得Sn-1=
an+n-3得Sn-1=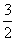 an-1+n-4,
an-1+n-4,
两式相减,得Sn-Sn-1=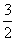 an-
an-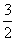 an-1+1,
an-1+1,
即an=3an-1-2,则an-1=3(an-1-1),
故数列{an-1}是以a1-1=3为首项,3为公比的等比数列.
(2)由(1)知an-1=3n,
cn=log3(a1-1)+log3(a2-1)+…+log3(an-1)=1+2+…+n= ,所以
,所以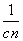 =
=
则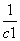 +
+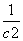 +…+
+…+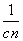
 由
由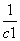 +
+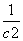 +…+
+…+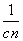 ≥
≥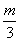 对任意n∈N*都成立,得
对任意n∈N*都成立,得 对任意n∈N*都成立,又m∈N*,所以m的值为1,2,3.
对任意n∈N*都成立,又m∈N*,所以m的值为1,2,3.

练习册系列答案
相关题目
 ,则
,则 =( )
=( ) B.
B.
 D.30
D.30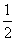 ,a6+a7=3.则满足a1+a2+…+an>a1a2…an的最大正整数n的值为________.
,a6+a7=3.则满足a1+a2+…+an>a1a2…an的最大正整数n的值为________.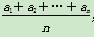 ,n∈N*,则数列{bn}的前n项和是( )
,n∈N*,则数列{bn}的前n项和是( ) ,记Tn=-b1+b2-b3+b4-…+(-1)nbn,求Tn.
,记Tn=-b1+b2-b3+b4-…+(-1)nbn,求Tn. ,其中n为正整数.
,其中n为正整数.