函数y=$\sqrt{x-1}+\frac{1}{3-x}$的定义域是{x|x≥1且x≠3}．题目和参考答案——青夏教育精英家教网——

题目内容

8．函数y=$\sqrt{x-1}+\frac{1}{3-x}$的定义域是{x|x≥1且x≠3}．

分析函数y=$\sqrt{x-1}+\frac{1}{3-x}$有意义，只需x-1≥0，且3-x≠0，解不等式即可得到所求．

解答解：函数y=$\sqrt{x-1}+\frac{1}{3-x}$有意义，
只需x-1≥0，且3-x≠0，
解得x≥1且x≠3，
则定义域为{x|x≥1且x≠3}，
故答案为：{x|x≥1且x≠3}．

点评本题考查函数的定义域的求法，注意偶次根式和分式的含义，属于基础题．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

18．若${log_a}\frac{4}{5}＜1$（a＞0，且a≠1），则实数a的取值范围是（　　）

$（0，\frac{4}{5}）$

$（\frac{4}{5}，+∞）$

$（\frac{4}{5}，1）$

$（0，\frac{4}{5}）∪（1，+∞）$

19．已知S_n为等比数列{a_n}的前n项和，且S₅=S₄-2a₄，则$\frac{{S}_{5}}{{S}_{4}}$等于（　　）

-$\frac{33}{15}$

$\frac{33}{15}$

-$\frac{33}{17}$

$\frac{33}{17}$

16．如果集合U={1，2，3，4，5，6，7，8}，A={2，3，5，8}，B={1，3，5，7}，那么（∁_UA）∩B等于（　　）

{1，3，4，5，6，7，8}

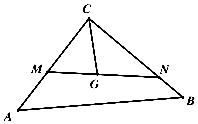如图，等腰直角三角形ABC，点G是△ABC的重心，过点G作直线与CA，CB两边分别交于M，N两点，且$\overrightarrow{CM}=λ\overrightarrow{CA}$，$\overrightarrow{CN}=μ\overrightarrow{CB}$，则λ+4μ的最小值为3．

13．已知x∈（0，+∞）有下列各式：x+$\frac{1}{x}$≥2，x+$\frac{4}{{x}^{2}}$=$\frac{x}{2}$+$\frac{x}{2}$+$\frac{4}{{x}^{2}}$≥3，x+$\frac{27}{{x}^{3}}$=$\frac{x}{3}$+$\frac{x}{3}$+$\frac{x}{3}$+$\frac{27}{{x}^{3}}$≥4成立，观察上面各式，按此规律若x+$\frac{a}{{x}^{4}}$≥5，则正数a=4⁴．

20．设正数x，y满足x²+$\frac{{y}^{2}}{2}$=1，则x•$\sqrt{1+{y}^{2}}$的最大值为（　　）

$\frac{3\sqrt{2}}{2}$

$\frac{3\sqrt{2}}{4}$

17．已知等差数列{a_n}满足a₁+a₂+a₃+…+a₁₀₁=0，则a₅₁=0．

18．实数a=0.3³，b=log₃0.3，c=3^0.3的大小关系是（　　）