题目内容
若α为锐角,且sin(α-
)=
,则sinα的值为 .
| π |
| 6 |
| 1 |
| 3 |
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:先利用同角三角函数基本关系求得cos(α-
)进而根据sinα=sin(α-
+
)利用正弦的两角和公式求得答案.
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
解答:
解:∵0<α<
,
∴-
<α-
<
,
∴cos(α-
)=
=
,
∴sinα=sin(α-
+
)=sin(α-
)cos
+cos(α-
)sin
=
×
+
×
=
,
故答案为:
.
| π |
| 2 |
∴-
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
∴cos(α-
| π |
| 6 |
1-sin2(α-
|
2
| ||
| 3 |
∴sinα=sin(α-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 3 |
| ||
| 2 |
2
| ||
| 3 |
| 1 |
| 2 |
| ||||
| 6 |
故答案为:
| ||||
| 6 |
点评:本题主要考查了两角和与差的正弦函数公式的应用.解题的关键时构造出α-
+
.
| π |
| 6 |
| π |
| 6 |

练习册系列答案
相关题目
已知正四棱锥O-ABCD中,OA=AB,则OA与底面ABCD所成角的正弦值等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
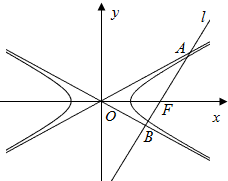 如图所示,已知双曲线
如图所示,已知双曲线| x2 |
| a2 |
| y2 |
| b2 |
| AF |
| FB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知双曲线
-
=1(a>0,b>0)的一条渐近线方程为x-2y=0,则该双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 三棱柱ABC-A1B1C1体积为V,M是AA1中点,求四棱锥M-BCC1B1的体积.
三棱柱ABC-A1B1C1体积为V,M是AA1中点,求四棱锥M-BCC1B1的体积.