题目内容
已知球的半径为5，球面被互相垂直的两个平面所截，得到的两个圆的公共弦长为2
，若其中一个圆的半径为4，则另一个圆的半径为 ．
| 3 |
考点：球的体积和表面积
专题：空间位置关系与距离
分析：可以从三个圆心上找关系，构建矩形利用对角线相等即可求解出答案．
解答：
解：设两圆的圆心分别为O1、O2，球心为O，公共弦为AB，其中点为E，则OO1EO2为矩形，
于是OO1=O2E=
=
=3，
AE=
AB=
∴O2A═
=
=2
∴圆O2的半径为2
．
故答案为：2
．
解：设两圆的圆心分别为O1、O2，球心为O，公共弦为AB，其中点为E，则OO1EO2为矩形，于是OO1=O2E=
| OA2-O1A2 |
| 25-16 |
AE=
| 1 |
| 2 |
| 3 |
∴O2A═
| AE2-O2E2 |
| 3+9 |
| 3 |
∴圆O2的半径为2
| 3 |
故答案为：2
| 3 |
点评：本题主要考查球的有关概念以及两平面垂直的性质，是对基础知识的考查．解决本题的关键在于得到OO1EO2为矩形．
练习册系列答案
相关题目
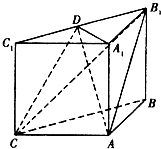如图，三棱柱ABC-A1B1C1中，A1A⊥底面ABC，AC=AB=AA1=4，∠BAC=90°，点D是棱B1C1的中点．
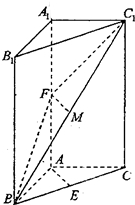如图，在三棱柱ABC-A1B1C1中，A1A⊥面ABC，∠BAC=90°，E为BC的中点，F为A1A的中点，A1A=4，AB=AC=2．
已知正方体ABCD-A1B1C1D1的各棱长为2，则D1到面AB1C的距离为已知正四棱锥O-ABCD中，OA=AB，则OA与底面ABCD所成角的正弦值等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|