题目内容
已知直线l1:x+y-
=0,l2:x+y-4
=0,⊙C的圆心到l1,l2的距离依次为d1,d2且d2=2d1,⊙C与直线l2相切,则直线l1被⊙C所截得的弦长为 .
| 2 |
| 2 |
考点:直线与圆相交的性质
专题:计算题,直线与圆
分析:求出直线l1:x+y-
=0,l2:x+y-4
=0的距离,利用⊙C的圆心到l1,l2的距离依次为d1,d2且d2=2d1,可得d1=1,d2=2或d1=3,d2=6,结合⊙C与直线l2相切,即可求出直线l1被⊙C所截得的弦长.
| 2 |
| 2 |
解答:
解:直线l1:x+y-
=0,l2:x+y-4
=0的距离为
=3,
∵⊙C的圆心到l1,l2的距离依次为d1,d2且d2=2d1,
∴d1=1,d2=2或d1=3,d2=6,
∵⊙C与直线l2相切,
∴直线l1被⊙C所截得的弦长为2
=2
或2
=6
.
故答案为:2
或6
.
| 2 |
| 2 |
|-
| ||||
|
∵⊙C的圆心到l1,l2的距离依次为d1,d2且d2=2d1,
∴d1=1,d2=2或d1=3,d2=6,
∵⊙C与直线l2相切,
∴直线l1被⊙C所截得的弦长为2
| 22-12 |
| 3 |
| 62-32 |
| 3 |
故答案为:2
| 3 |
| 3 |
点评:本题考查两条平行线距离的求法,考查直线与圆相交的性质,正确分类是关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
函数f(x)=3x-x3的单调递增区间是( )
| A、[-1,1] | ||||
| B、[1,+∞)∪(-∞,-1] | ||||
| C、[1,+∞)及(-∞,-1] | ||||
D、[-
|
已知正四棱锥O-ABCD中,OA=AB,则OA与底面ABCD所成角的正弦值等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
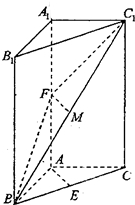 如图,在三棱柱ABC-A1B1C1中,A1A⊥面ABC,∠BAC=90°,E为BC的中点,F为A1A的中点,A1A=4,AB=AC=2.
如图,在三棱柱ABC-A1B1C1中,A1A⊥面ABC,∠BAC=90°,E为BC的中点,F为A1A的中点,A1A=4,AB=AC=2. 已知正方体ABCD-A1B1C1D1的各棱长为2,则D1到面AB1C的距离为
已知正方体ABCD-A1B1C1D1的各棱长为2,则D1到面AB1C的距离为
 三棱柱ABC-A1B1C1体积为V,M是AA1中点,求四棱锥M-BCC1B1的体积.
三棱柱ABC-A1B1C1体积为V,M是AA1中点,求四棱锥M-BCC1B1的体积.