题目内容
如果函数f(x)的图象与函数g(x)=(
)x的图象关于直线y=x对称,则f(3x-x2)的单调递减区间是 .
| 1 |
| 2 |
考点:反函数
专题:函数的性质及应用
分析:函数f(x)的图象与函数g(x)=(
)x的图象关于直线y=x对称,可得f(x)=log
x,因此f(3x-x2)=log
(3x-x2)=log
(-(x-
)2+
)的单调递减区间满足
,解出即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
|
解答:
解:∵函数f(x)的图象与函数g(x)=(
)x的图象关于直线y=x对称,
∴函数f(x)是g(x)的反函数,
∴f(x)=log
x,
∴f(3x-x2)=log
(3x-x2)=log
(-(x-
)2+
)的单调递减区间满足
,解得0<x≤
.
故答案为:(0,
].
| 1 |
| 2 |
∴函数f(x)是g(x)的反函数,
∴f(x)=log
| 1 |
| 2 |
∴f(3x-x2)=log
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
|
| 3 |
| 2 |
故答案为:(0,
| 3 |
| 2 |
点评:本题考查了反函数、二次函数的单调性、对数函数的单调性、复合函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
若集合M={y|y=2-x},N={x|y=
},则M∩N等于( )
| x-1 |
| A、{y|y>1} |
| B、{y|y≥1} |
| C、{y|y>0} |
| D、{y|y≥0} |
若两个等差数列{an},{bn}的前n项的和为An,Bn.且
=
,则
=( )
| An |
| Bn |
| 4n+5 |
| 5n-5 |
| a5+a13 |
| b5+b13 |
A、
| ||
B、
| ||
C、
| ||
D、
|
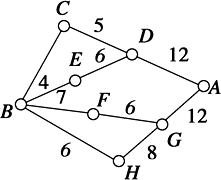 如图所示,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,已知单位时间内传递的最大信息量为19,则从结点C向结点B单位时间内可以通过的最大信息量为
如图所示,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,已知单位时间内传递的最大信息量为19,则从结点C向结点B单位时间内可以通过的最大信息量为