题目内容
若集合M={y|y=2-x},N={x|y=
},则M∩N等于( )
| x-1 |
| A、{y|y>1} |
| B、{y|y≥1} |
| C、{y|y>0} |
| D、{y|y≥0} |
考点:指数函数单调性的应用,交集及其运算
专题:计算题,函数的性质及应用,集合
分析:由y=2-x>0,可化简M,由x-1≥0,可化简N,再求交集即可.
解答:
解:由y=2-x>0,得M={y|y=2-x}={y|y>0},
由x-1≥0得x≥1,则N={x|x≥1},
则有M∩N={y|y≥1},
故选B.
由x-1≥0得x≥1,则N={x|x≥1},
则有M∩N={y|y≥1},
故选B.
点评:本题考查集合的化简,注意集合中代表元素的含义,考查运算能力,属于基础题和易错题.

练习册系列答案
相关题目
数列{an}满足a1=2,an=
,其前n项积为Tn,则T2015=( )
| an+1-1 |
| an+1+1 |
| A、2 | B、1 | C、3 | D、-6 |
在△ABC中,角A,B,C的对边分别是a,b,c,若a=2
,A=45°,B=60°,则b=( )
| 2 |
A、2
| ||
B、
| ||
| C、1 | ||
| D、2 |
袋子里装有大小相同的黑白两色的手套,黑色手套15支,白色手套10只,现从中随机地取出2只手套,如果2只是同色手套则甲获胜,2只手套颜色不同则乙获胜.试问:甲、乙获胜的机会是( )
| A、甲多 | B、乙多 |
| C、一样多 | D、不确定 |
设p:x<-1或x>1;q:x<-2或x>1,则¬p是¬q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既充分也不必要条件 |
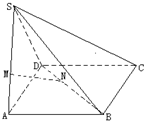 如图,已知S是平行四边形ABCD所在平面外一点,M,N分别是SA,BD上的点,MN=5,AB=AD=SB=SA=6,且
如图,已知S是平行四边形ABCD所在平面外一点,M,N分别是SA,BD上的点,MN=5,AB=AD=SB=SA=6,且