题目内容
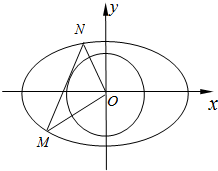 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
| 1 |
| 2 |
(Ⅰ)求椭圆C方程;
(Ⅱ)若直线MN与圆O:x2+y2=
| 1 |
| 25 |
(Ⅲ)在(Ⅱ)的条件下,求|OM|•|ON|的取值范围.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知得2a=
,2b=
,由此能求出椭圆C的方程.
(Ⅱ)当直线MN⊥x轴时,∠MON=
.当直线MN与x轴不垂直时,设直线MN:y=kx+b,直线MN与与圆O:x2+y2=
的交点M(x1,y1),N(x2,y2),由直线MN与圆O相切,得25b2=k2+1,联立
,得(9+16k2)x2+32kbx+16b2-1=0,由此能证明∠MON=
为定值.
(Ⅲ)设∠XOM=θ,则∠XON=θ±
,由三角函数定义知M(|OM|cosθ,|OM|sinθ),N(±|ON|sinθ,±|ON|cosθ),从而
=(9cos2θ+16sin2θ)(9sin2θ+16cos2θ)=9×16+(9-16)2•
sin22θ,由此能求出|OM|的取值范围.
| 2 |
| 3 |
| 1 |
| 2 |
(Ⅱ)当直线MN⊥x轴时,∠MON=
| π |
| 2 |
| 1 |
| 25 |
|
| π |
| 2 |
(Ⅲ)设∠XOM=θ,则∠XON=θ±
| π |
| 2 |
| 1 |
| |OM|2 |
| 1 |
| 4 |
解答:
(Ⅰ)解:由椭圆C:
+
=1(a>b>0)上点到两焦点距离和为
,
得2a=
,即a=
;
由短轴长为
,得2b=
,即b=
.
∴椭圆C的方程为:9x2+16y2=1.
(Ⅱ)证明:当直线MN⊥x轴时,∵直线MN与圆O:x2+y2=
相切,
∴直线MN方程为:x=
或x=-
,
当直线方程为x=
,得两点分别为(
,
)和(
,-
),
故
•
=0,∠MON=
.
同理当x=-
时,∠MON=
.
当直线MN与x轴不垂直时,设直线MN:y=kx+b,直线MN与与圆O:x2+y2=
的交点M(x1,y1),N(x2,y2),
由直线MN与圆O相切得d=
=
,即25b2=k2+1,①
联立
,得(9+16k2)x2+32kbx+16b2-1=0,
∴△>0,x1+x2=-
,x1x2=
,
由
•
=x1x2+y1y2=x1x2+(kx1+b)(kx2+b)
=(1+k2)x1x2+kb(x1+x2)+b2
=
,②
由①②,得
•
=0,即∠MON=
,
综上,∠MON=
为定值.
(Ⅲ)解:不妨设∠XOM=θ,则∠XON=θ±
,
由三角函数定义知M(|OM|cosθ,|OM|sinθ),N(±|ON|sinθ,±|ON|cosθ),
∵M,N都在9x2+16y2=1上,
∴
=(9cos2θ+16sin2θ)(9sin2θ+16cos2θ)
=9×16+(9-16)2sin2θcos2θ
=9×16+(9-16)2•
sin22θ,
又sin22θ∈[0,1],故(
•
)2∈[9×16,(
)2],
∴|OM|的取值范围是[
,
].
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
得2a=
| 2 |
| 3 |
| 1 |
| 3 |
由短轴长为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴椭圆C的方程为:9x2+16y2=1.
(Ⅱ)证明:当直线MN⊥x轴时,∵直线MN与圆O:x2+y2=
| 1 |
| 25 |
∴直线MN方程为:x=
| 1 |
| 5 |
| 1 |
| 5 |
当直线方程为x=
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
故
| OM |
| ON |
| π |
| 2 |
同理当x=-
| 1 |
| 5 |
| π |
| 2 |
当直线MN与x轴不垂直时,设直线MN:y=kx+b,直线MN与与圆O:x2+y2=
| 1 |
| 25 |
由直线MN与圆O相切得d=
| |b| | ||
|
| 1 |
| 5 |
联立
|
∴△>0,x1+x2=-
| 32kb |
| 9+16k2 |
| 16b2-1 |
| 9+16k2 |
由
| OM |
| ON |
=(1+k2)x1x2+kb(x1+x2)+b2
=
| 25b2-k2-1 |
| 9+16k2 |
由①②,得
| OM |
| ON |
| π |
| 2 |
综上,∠MON=
| π |
| 2 |
(Ⅲ)解:不妨设∠XOM=θ,则∠XON=θ±
| π |
| 2 |
由三角函数定义知M(|OM|cosθ,|OM|sinθ),N(±|ON|sinθ,±|ON|cosθ),
∵M,N都在9x2+16y2=1上,
∴
| 1 |
| |OM|2 |
=9×16+(9-16)2sin2θcos2θ
=9×16+(9-16)2•
| 1 |
| 4 |
又sin22θ∈[0,1],故(
| 1 |
| |OM| |
| 1 |
| |ON| |
| 9+16 |
| 2 |
∴|OM|的取值范围是[
| 2 |
| 25 |
| 1 |
| 12 |
点评:本题考查椭圆方程的求法,考查角为定值的证明,考查线段的取值范围的求法,是中档题,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
已知α,β是平面,a,b,c是直线,O是点.下列五个命题:
①若α∥β,a?α,b?β,则a∥b;
②若a∥b,a⊥c,则b⊥c;
③若a∥α,b?α,则a∥b;
④若a∥α,b∥α,则a∥b;
⑤若a∩b=O,a∥α,则b与α平行或相交.
其中正确的有( )
①若α∥β,a?α,b?β,则a∥b;
②若a∥b,a⊥c,则b⊥c;
③若a∥α,b?α,则a∥b;
④若a∥α,b∥α,则a∥b;
⑤若a∩b=O,a∥α,则b与α平行或相交.
其中正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
方程2sin2x=x-3的解有( )个.
| A、1 | B、2 | C、3 | D、4 |
下列说法错误的是( )
| A、在统计里,从总体中抽取的一部分个体叫做总体的一个样本,样本中个体的数目叫做样本的容量 |
| B、一组数据的平均数一定大于这组数据中的每个数据 |
| C、平均数、众数与中位数从不同的角度描述了一组数据的集中趋势 |
| D、一组数据的方差越大,说明这组数据的波动性越大 |
已知Sn是等差数列{an}的前n项和,a1=1,S5=25,设Tn为数列{(-1)n+1an}的前n项和,则T2015=( )
| A、2014 | B、-2014 |
| C、2015 | D、-2015 |
曲线
+
=1与曲线
+
=1(m<3)的( )
| x2 |
| 4 |
| y2 |
| 3 |
| x2 |
| 4-m |
| y2 |
| 3-m |
| A、长轴长相等 | B、短轴长相等 |
| C、离心率相等 | D、焦距相等 |
已知a>0且a≠1,下列四组函数中表示相等函数的是( )
| A、y=logax与y=(logxa)-1 |
| B、y=2x与y=logaa2x |
| C、y=alogax与y=x |
| D、y=logax2与y=2logax |
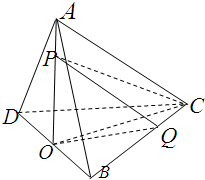 如图,在三棱锥A-BCD中,BC=DC=AB=AD=2,BD=2,平面ABD⊥平面BCD,O为BD中点,点P,Q分别为线段AO,BC上的动点(不含端点),且AP=CQ,则三棱锥P-QCO体积的最大值为
如图,在三棱锥A-BCD中,BC=DC=AB=AD=2,BD=2,平面ABD⊥平面BCD,O为BD中点,点P,Q分别为线段AO,BC上的动点(不含端点),且AP=CQ,则三棱锥P-QCO体积的最大值为