题目内容
已知y=f(x)+2x为奇函数,且g(x)=f(x)+1.若f(2)=2,则g(-2)= .
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据奇函数得出f(2)+22=-[f(-2)+2-2],即f(-2)=-
,即可求解g(-2).
| 25 |
| 4 |
解答:
解:∵y=f(x)+2x为奇函数,
∴f(2)+22=-[f(-2)+2-2],
得f(-2)=-
∴g(-2)=f(-2)+1=-
.
故答案为:-
,
∴f(2)+22=-[f(-2)+2-2],
得f(-2)=-
| 25 |
| 4 |
∴g(-2)=f(-2)+1=-
| 21 |
| 4 |
故答案为:-
| 21 |
| 4 |
点评:本题考查了利用函数的奇偶性求解函数值,整体思想的运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知实数m,n满足m2+n2=2,则点P(m+n,m-n)的轨迹方程是( )
| A、x2+y2=1 |
| B、x2-y2=1 |
| C、x2+y2=2 |
| D、x2+y2=4 |
若x+2y=4,则2x+4y的最小值是( )
| A、4 | ||
| B、8 | ||
C、2
| ||
D、4
|
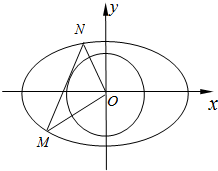 已知椭圆C:
已知椭圆C: 随机抽取100名年龄在[10,20),[20,30),…[50,60)年龄段的市民进行问卷调查,由此得到样本的频率分布直方图如图所示,从不小于40岁的人中按年龄段分层抽样的方法随机抽取8人,则在[50,60)年龄段抽取的人数为
随机抽取100名年龄在[10,20),[20,30),…[50,60)年龄段的市民进行问卷调查,由此得到样本的频率分布直方图如图所示,从不小于40岁的人中按年龄段分层抽样的方法随机抽取8人,则在[50,60)年龄段抽取的人数为