题目内容
已知a>0且a≠1,下列四组函数中表示相等函数的是( )
| A、y=logax与y=(logxa)-1 |
| B、y=2x与y=logaa2x |
| C、y=alogax与y=x |
| D、y=logax2与y=2logax |
考点:判断两个函数是否为同一函数
专题:计算题,函数的性质及应用
分析:由题意,判断函数的定义域与对应关系是否相同即可.
解答:
解:A:y=logax的定义域为(0,+∞),
y=(logxa)-1的定义域为(0,1)∪(1,+∞);
故不相等;
B:y=2x的定义域为R,
y=logaa2x=2x的定义域为R;
故相等;
C:y=alogax的定义域为(0,+∞),
y=x的定义域为R;
故不相等;
D:y=2logax的定义域为(0,+∞),
y=logax2的定义域为(-∞,0)∪(0,+∞);
故不相等.
故选B.
y=(logxa)-1的定义域为(0,1)∪(1,+∞);
故不相等;
B:y=2x的定义域为R,
y=logaa2x=2x的定义域为R;
故相等;
C:y=alogax的定义域为(0,+∞),
y=x的定义域为R;
故不相等;
D:y=2logax的定义域为(0,+∞),
y=logax2的定义域为(-∞,0)∪(0,+∞);
故不相等.
故选B.
点评:本题考查了函数相等的判断,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
若x+2y=4,则2x+4y的最小值是( )
| A、4 | ||
| B、8 | ||
C、2
| ||
D、4
|
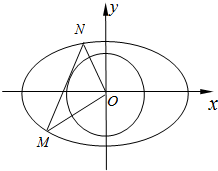 已知椭圆C:
已知椭圆C: 随机抽取100名年龄在[10,20),[20,30),…[50,60)年龄段的市民进行问卷调查,由此得到样本的频率分布直方图如图所示,从不小于40岁的人中按年龄段分层抽样的方法随机抽取8人,则在[50,60)年龄段抽取的人数为
随机抽取100名年龄在[10,20),[20,30),…[50,60)年龄段的市民进行问卷调查,由此得到样本的频率分布直方图如图所示,从不小于40岁的人中按年龄段分层抽样的方法随机抽取8人,则在[50,60)年龄段抽取的人数为