题目内容
已知Sn是等差数列{an}的前n项和，a1=1，S5=25，设Tn为数列{（-1）n+1an}的前n项和，则T2015=（ ）
| A、2014 | B、-2014 |
| C、2015 | D、-2015 |
考点：数列的求和
专题：等差数列与等比数列
分析：求出数列的通项公式，然后写出所求表达式，通过相邻两项合并，求解即可．
解答：
解：∵S5=5a3=25，∴a3=5，又a1=1，
所以公差d=2，an=2n-1，
所以T2015=（a1-a2）+（a3-a4）+（a5-a6）+…+（a2013-a2014）+a2015
=-1007d+a2015=2015，
故选C．
所以公差d=2，an=2n-1，
所以T2015=（a1-a2）+（a3-a4）+（a5-a6）+…+（a2013-a2014）+a2015
=-1007d+a2015=2015，
故选C．
点评：本题考查数列的求和，相邻两项合并得到新数列是解题的关键，考查计算能力．
练习册系列答案
相关题目
设函数f（x）的导函数为f′（x），对任意x∈R都有f（x）＞f′（x）成立，则（ ）
| A、3f（ln2）＞2f（ln3） |
| B、3f（ln2）=2f（ln3） |
| C、3f（ln2）＜2f（ln3） |
| D、3f（ln2）与2f（ln3）的大小不确定 |
在如图所示的“茎叶图”表示的数据中，众数和中位数分别（ ）
| A、23和26 |
| B、31和26 |
| C、24和30 |
| D、26和30 |
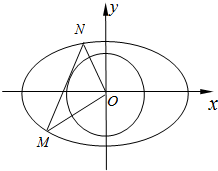已知椭圆C：