题目内容
下列函数中,满足“f(x+y)=f(x)f(y)”的单调递增函数是( )
| A、f(x)=x3 | ||
| B、f(x)=3x | ||
C、f(x)=x
| ||
D、f(x)=(
|
考点:抽象函数及其应用
专题:函数的性质及应用
分析:对选项一一加以判断,先判断是否满足f(x+y)=f(x)f(y),然后考虑函数的单调性,即可得到答案.
解答:
解:A.f(x)=x3,f(y)=y3,f(x+y)=(x+y)3,不满足f(x+y)=f(x)f(y),故A错;
B.f(x)=3x,f(y)=3y,f(x+y)=3x+y,满足f(x+y)=f(x)f(y),且f(x)在R上是单调增函数,故B正确;
C.f(x)=x
,f(y)=y
,f(x+y)=(x+y)
,不满足f(x+y)=f(x)f(y),故C错;
D.f(x)=(
)x,f(y)=(
)y,f(x+y)=(
)x+y,满足f(x+y)=f(x)f(y),但f(x)在R上是单调减函数,故D错.
故选B.
B.f(x)=3x,f(y)=3y,f(x+y)=3x+y,满足f(x+y)=f(x)f(y),且f(x)在R上是单调增函数,故B正确;
C.f(x)=x
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
D.f(x)=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选B.
点评:本题主要考查抽象函数的具体模型,同时考查幂函数和指数函数的单调性,是一道基础题.

练习册系列答案
相关题目
将函数y=3sin(2x+
)的图象向右平移
个单位长度,所得图象对应的函数( )
| π |
| 3 |
| π |
| 2 |
A、在区间[
| ||||
B、在区间[
| ||||
C、在区间[-
| ||||
D、在区间[-
|
某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
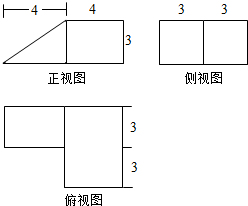

| A、72cm3 |
| B、90cm3 |
| C、108cm3 |
| D、138cm3 |
| 1+3i |
| 1-i |
| A、1+2i | B、-1+2i |
| C、1-2i | D、-1-2i |
等差数列{an}的公差为2,若a2,a4,a8成等比数列,则{an}的前n项和Sn=( )
| A、n(n+1) | ||
| B、n(n-1) | ||
C、
| ||
D、
|